結合強度の求め方

ホップフィールドネットの結合強度をエネルギー関数から求める方法。 この方法は与えられた問題が最適化問題に置き換えられるときに有効で、 最小化する目的関数とネットワークのエネルギー関数を比較することで結合強度 を求める。

説明を簡単にするために、ホップフィールドネットに与えられたアナログ値を4 ビットのディジタル値に変換する A/D 変換問題を考える。 ネットワークは 4 ユニットで構成され、それらの状態 は変換 後のディジタル値 (0 or 1) を表すものとする。また、変換するアナログ値はネッ トワークの外部入力として提示される。このようなネットワークが A/D 変換器 として機能を持つためには、入力されるアナログ値 a とすると、以下のエネル ギー関数を最小化すればよい。

 

ここで は 0 から 3 までで i に等しく ない添字 j に関して加え合わせることを意味する。 で外部入力 考慮したネットワークのエネルギー関数は

 

式(27) と式(28) とを比較すると

与えれたエネルギー関数がリアプノフ関数 Lyapunov function の条件を満たす ように、エネルギー関数から直接的にネットワークダイナミックスを求める方法 もある。これは、まず式(27) の時間微分を求めて

 

ネットワークのエネルギーが時間とともに減少するためには の関係が常に満たされればよい。このためには、以下に示すように を式(31)の[]内の式に等しくすればよい

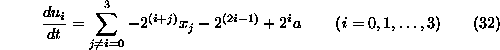
このとき

となり を単調増加関数とすれば が満たされるこ とがわかる。

この結果は先の式と一致する。