ボルツマンマシン Boltzmann machine

Hinton, Sejnowski らによって提案された確率的に動作するニューラルネット ワークです。

ホップフィールドネットでは、ローカルミニマムに陥ると抜け出すことができな かった訳ですが、各ユニットを確率的に動作させることによって、ローカルミニ マムの問題を回避させるように工夫されたものです。

各ユニット間の結合係数は対称 , 自己結合はなし を仮定するのはホップフィールドと同じです。各ユニットの出力は 0 または 1 を取りますが、どちらになるかが決定論的に決まるのではなく 1 を出力する 確率が次のように定義されます。

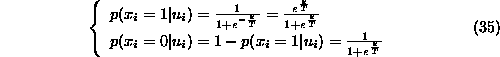
T は温度 と呼ばれる定数(;SPMgt;0)で、 温度が低くなると、0 付近で傾きが急になり の極限では ホップフィールドモデルに一致します。 逆に 温度が高くなると が 1 になる確率がなだらかになります。

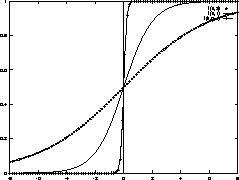
では によらず が 1 になるか 0 になるかは 1/2 になります。 すなわち`熱雑音が大きくなると系の不確定性が増す'ということです。

今 n 個のニューロンを考えた場合ネットワーク全体の状態 は全部で 通り存在します。

ネットワークが時刻 t で状態 (たとえば など) に なったとします。次の時刻 t+1 で別の状態 になる遷移確率は、

 

と表せます 。 はすべての状態についての総和の意味です。 式(37) を簡単にするために、 を縦に並べて全部で この要素の列ベクトルを作ると 行 列を要素とする行列 P ができます。すると式 (37)は

と表すことができ、P のことを状態遷移行列といいます。状態遷移行列 P が時 刻によらないものならば時刻 t+1 における確率分布 は によっ て完全に記述できます。このような確率過程をマルコフ Markov 連鎖といいます 。

ネットワークの状態が p=Pp のように時刻によらない形になっている場合、 定常状態といいます。定常状態になっている場合の の出現確率は

で与えられます。この形をした確率密度関数に従う分布を 統計物理学ではボルツマン Boltzmann 分布といいます。 は状態 に対するエネルギーで

となります。ここで c は となるように規格化するための 定数です。具体的には

です。

定常確率分布がボルツマン分布に従うことの証明
i 番目のニューロンの値を とし、次の時刻でのこのニューロンの出力を とします。確率的に定常な状態ならば、

 

が成立します。一回に一つのニューロンしか変化しないので他のニューロンは無 視します。 がボルツマン分布に従うと仮定したときに式 (42)が成立することを証明します。 次の時刻で 1 を出力する確率は、

 

となります。ここで、変化前の分布がボルツマン分布に従うと仮定すると、

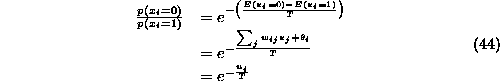
となるので、これをを式(43)に代入すれば が証明できました。

このように定常状態 p の出現確率はネットワークの各状態に対して 計算されるエネルギー E によって決まり、その確率がボルツマン分布に従うこ とからこのネットワークのことをボルツマンマシンといいます。

ただし、ネットワークのサイズ(ニューロンの数)が大きくなると定常分布を実際 に計算するのは計算量が多くて大変な作業になり、実際に計算するのはほぼ不可 能です。そこでシミュレーションの出番になるわけです。

ボルツマンマシンにおいては、ホップフィールドモデルの持っていた 問題点-ローカルミニマムからの脱出できる可能性を持っています。 温度 T が大きければ、ローカルミニマムから脱出する確率が増します。 ところが、

1. 温度を高くするとエネルギー最小の状態をとる確率が低くなってしまう。
2. 温度を低くするとエネルギー最小の状態になる確率が高くなるが、定常 状態になるまで時間がかかる

という問題があります。そこではじめは温度の高い状態から出発して、しだいに 温度を下げていくという方法を採ることがあります。この方法のことを シミュレーティッドアニーリング simulated annealing (シミュレーションによ る焼きなまし、疑似徐冷)といいます。温度の低下を時間の関数として

のようにすることで、最小値に達することが Geman によって証明されています。 Gemanらの論文は、画像処理にランダムマルコフ場を導入した画期的なもので ボルツマンマシンの応用例と見なすことができます。

ボルツマンマシンの学習アルゴリズム
次のような入力層、中間層、出力層が全結合したネットワークを考えます。

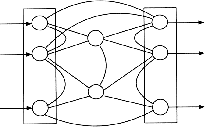
簡単にまとめるとボルツマンマシンの学習アルゴリズムは以下のようになります。

学習フェーズ

1. 結合係数を乱数で初期化する
2. 任意の入力ベクトルと出力ベクトルの組をネットワークに与える
3. シミュレーティドアニーリングによってシステムの定常状態にする
4. , がともに発火している場合結合係数 を一定量増 加させる
5. 2-4 を繰り返す

反学習フェーズ

1. 任意の入力ベクトルをネットワークに与える。このとき出力層は すべて 0 にする。
2. シミュレーティドアニーリングによってシステムの定常状態にする
3. , がともに発火している場合結合係数 を 一定量減少させる
4. 1-3 を繰り返す

Crick & Mitchison は哺乳類の REM 睡眠で逆転学習が起きると考えました。彼 らによれば、哺乳類は活動しているときに脳のシステムが巨大であるあために分 散記憶を妨げるような副次モードが発生します。脳にとって不適切なモードが 睡眠期に起こる不規則な興奮状態によって取り除かれるのではないか、というの が彼らの提案です。Hinton & Sejnowski は Crick らの仮説がボルツマンマシ ンの二つの学習フェーズに対応する可能性を指摘しました。

その他にも、ネットワークの一部が壊れても自発的に回復する機能などが実現で きることが指摘されています。