前回の予告通り、今日は2標本の検定を行いますが、その前に、 F 分布と F 検定について説明します。 2標本の検定方法は2種類あり、どちらを選ぶかは F 検定で決まるからです。 なお、次回以降説明する分散分析では、 F 検定を使っています。
F分布 ( F-distribution )とは、確率分布の一種で、次の性質を持ちます。 標本 X の大きさを n 1 , 分散を s 1 2 , 標本 Y の大きさを n 2 , 分散を s 2 2 とすると、2つの分散の比 F = s 1 2 / s 2 2 は自由度( n 1 −1, n 2 −1) の F 分布に従う。
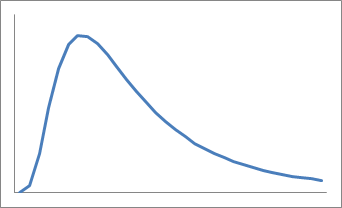
t 分布のときは、自由度 n −1というパラメータを1つ持ちましたが、 F 分布では自由度( n 1 −1, n 2 −1)とパラメータを2つ持ちます。 前者を分子の自由度、後者を分母の自由度と呼ぶことがあります。 以下は、自由度(11,7)の F 分布のグラフです。

F検定 ( F-test )とは、分散比 F = s 1 2 / s 2 2 を検定統計量とした検定です。 F 検定を行うと、散らばりに差があるかどうかが分かります。 つまり、帰無仮説は母分散が等しい、対立仮説は母分散が等しくない、とします。 そして、分散比 F が10倍や100倍という大きな数になったり、0.1倍や0.01倍という小さな数になったりして、有意水準未満の確率でしか発生しない場合(これを有意であると言います)、母分散が等しいという帰無仮説は棄却され、母分散が等しくないという対立仮説が採択されます。
前回、仮説検定は(1)信頼区間、(2)検定統計量、(3) p 値、のいずれかで行われると説明しました。 F 検定も基本的に同じなのですが、いくつかの注意点があります。
信頼区間による検定の場合、95%信頼区間に(ゼロではなく)1が入っていなければ、有意水準5%で有意であり、帰無仮説は棄却され、対立仮説が採択されます。
検定統計量による検定の場合、検定統計量は分散比 F です。 ただし、 F 分布は、正規分布や t 分布と違い、左右対称ではありません。 そのため、有意水準5%の両側検定を行う際には、 F 分布の上側2.5%点と下側2.5%点を別々に用意しておき、分散比 F が上側2.5%点より大きいか、下側2.5%点より小さいときに、有意水準5%で有意であり、帰無仮説は棄却され、対立仮説が採択されます。
p 値による検定の場合は、まったく同じで、 p 値が0.05未満であれば、有意水準5%で有意であり、帰無仮説は棄却され、対立仮説が採択されます。
したがって、統計解析ソフトが利用可能であれば、 p 値で検定を行うのが簡単です。
前回の授業では、対標本と2標本の違いについて説明しました。 同一人物の前後のデータなら対標本、他人同士のデータなら2標本です。 今日は、2標本のデータについて、母平均に差があるかどうかを検定してみます。
例えば、大都市の中学生と過疎地の中学生との間に、何か差があるかと考えます。 学力、体力、および部活動の3点に注目し、英語の得点、50m走のタイム、および部活動への参加率を標本調査したとします。
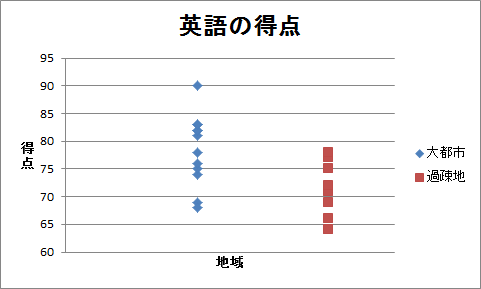
複数の標本の差を調べるとき、ドット・チャートを作成すると、視覚的に分かりやすくなります。 ここで、 ドット・チャート ( dot chart )とは、 ドット・プロット ( dot plot )とも呼ばれ、横軸をカテゴリー、縦軸を値にした散布図です。 ドット・チャートの点の集まりを見比べると、平均や散らばりの差が理解できます。 ドット・チャートの欠点は、重複した値が一つの点になってしまうことです。
ドット・チャートで大体の見当をつけたら、次に仮説検定を行います。 帰無仮説は大都市と過疎地には差がないとし、対立仮説は差があるとします。 2標本の場合、2つの差が余りにも大きく、有意水準未満の確率でしか発生しない場合(これを有意であると言います)、差がないという帰無仮説は棄却され、差があるという対立仮説が採択されます。 標本が小さいので、 t 検定を用います。
t 検定は、まず対標本か2標本かで分かれますが、2標本の場合も母分散が等しいか等しくないかで分かれます。 どの t 検定を利用するかは、以下のフローチャートに従ってください。
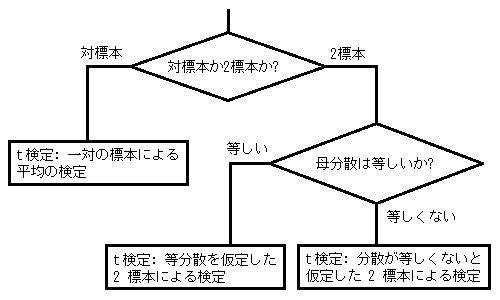
標本 X の大きさを n 1 , 平均を X , 標準偏差を s 1 , 標本 Y の大きさを n 2 , 平均を Y , 標準偏差を s 2 とします。 X と Y の母分散が等しい場合、「合併した標準偏差」
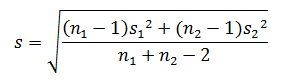
を定義すると、
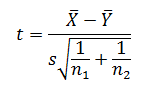
は、自由度 n 1 + n 2 −2の t 分布に従います。 したがって、検定統計量による検定なら、 t 統計量と両側5%点を比較すると、有意水準5%の両側検定が行えます。 t の定義式の分母は、2つの平均の差の標準誤差です。
母分散が等しくない場合は、 ウェルチの検定 ( Welch's test )と呼ばれる方法で検定を行います。 ウェルチの検定の t 統計量は、数式が複雑なので省略します。 また、自由度も n 1 + n 2 −2ではありません。 統計解析ソフトで計算してください。
母比率の差の検定というものも考えられます。
標本 X の大きさを n 1 , 比率を p 1 とし、標本 Y の大きさを n 2 , 比率を p 2 とします。 「合併した比率」 p を
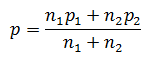
と定義すると、
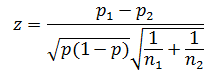
は、平均0、標準偏差1の正規分布に従うことが知られています。 したがって、 z の値と両側5%点を比較すると、有意水準5%の両側検定が行えます。
なお、 z の定義式の√( p ×(1− p ))を「合併した標準偏差」と見なし、分母を標準誤差と見なすと、母平均の差の検定と同じになります。
それでは、Excelを利用して、ドット・チャートを作成しましょう。 以下のExcelファイルをダウンロードしてください。
表「英語の得点」は、大都市の中学生と過疎地の中学生との間で、英語の得点に差があるかどうかを標本調査したものです。
まず、適宜コピー・アンド・ペーストして、Excelのデータを以下のような形式に変更します。 (1は大都市、2は過疎地です。)
この表全体をドラッグし、リボンの「挿入」をクリックし、「散布図」→「散布図」とクリックします。 すると、ドット・チャートが表示されます。
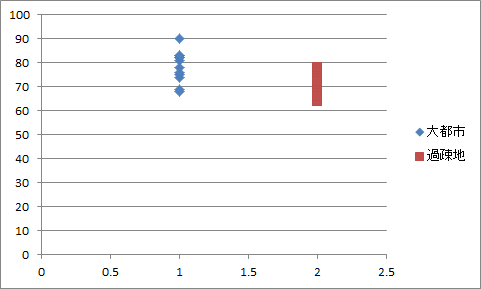
上側のグラフ・タイトルをダブル・クリックし、「英語の得点」に変更します。 (Windowsの場合は、グラフ・タイトルがないので、リボンの「レイアウト」をクリックし、「ラベル」項目で「グラフタイトル」→「グラフの上」とクリックします。) 凡例を右に移動するには、凡例を右クリックし、「凡例の書式設定」をクリックし、「凡例のオプション」→「凡例のオプション」とクリックして、「右」ラジオボタンをオンにします。 リボンの「グラフのデザイン」をクリックし、「グラフ要素を追加」→「軸ラベル」→「第1横軸」とクリックして、(Windowsの場合は、「ラベル」項目で「軸ラベル」→「主横軸ラベル」→「軸ラベルを軸の下に配置」とクリックして、)軸ラベルを「地域」に変更します。 同様に、「グラフ要素を追加」→「軸ラベル」→「第1縦軸」とクリックして、(Windowsの場合は、「ラベル」項目で「軸ラベル」→「主縦軸ラベル」→「軸ラベルを垂直に配置」とクリックして、)軸ラベルを「得点」に変更します。 軸ラベルを縦書きにするには、軸ラベルを右クリックし、「軸ラベルの書式設定」をクリックし、「タイトルのオプション」→「サイズとプロパティ」とクリックして、「テキストの方向」を「垂直」にします。
横軸をダブル・クリックすると、「軸の書式設定」ウィンドウを開くので、「軸のオプション」→「軸のオプション」とクリックし、「ラベル」をクリックして「ラベルの位置」を「なし」にしてください。 (Windowsの場合は「目盛の種類」と「軸ラベル」を「なし」にしてください。)
縦軸をダブル・クリックすると、「軸の書式設定」ウィンドウを開くので、「軸のオプション」→「軸のオプション」とクリックして、(Windowsの場合は「最小値」の「固定」ラジオ・ボタンをオンにしてから、)「最小値」入力欄に目盛の始まりの値(例えば60)を入力してください。
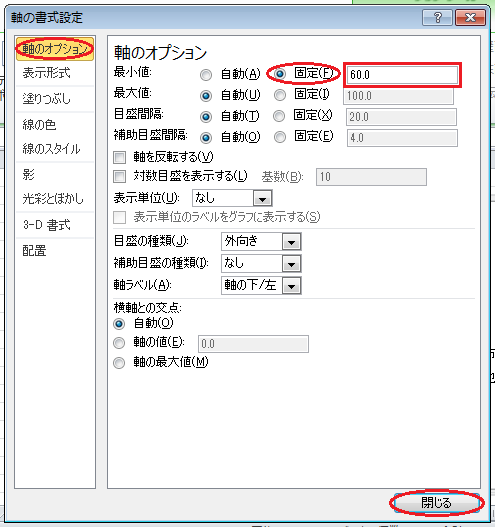
これで、ドット・チャートが完成します。

ドット・チャートを見ると、散らばりには差がなさそうですが、平均には差がありそうです。
「分析ツール」では、次の3種類の t 検定が利用可能です。
また、 F 検定については「F 検定: 2 標本を使った分散の検定」を利用します。
それでは、表「英語の得点」について、散らばりに差があるか確かめるために F 検定を行い、その後、平均に差があるか確かめるために t 検定を行います。
まず、母分散が等しいかどうかを確かめるために、 F 検定を行います。 帰無仮説は母分散が等しいとし、対立仮説は母分散が等しくないとします。 有意水準5%で両側検定を行います。
リボンの「データ」をクリックし、「データ分析」をクリックします。 すると、「データ分析」ウィンドウが開くので、「F 検定: 2 標本を使った分散の検定」をクリックして、「OK」ボタンをクリックします。
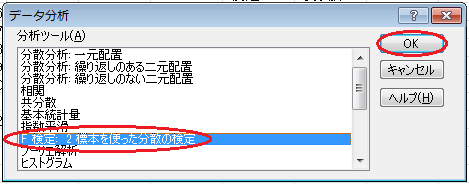
「変数 1 の入力範囲」に大都市のデータ$B$2:$B$14を入力し、「変数 2 の入力範囲」に過疎地のデータ$C$2:$C$10を入力します。 「ラベル」チェックボックスをオンにし、「α」入力欄に0.025を入力します。 「出力オプション」の「出力先」をクリックし、空いているセル(例えば$E$1)を入力します。
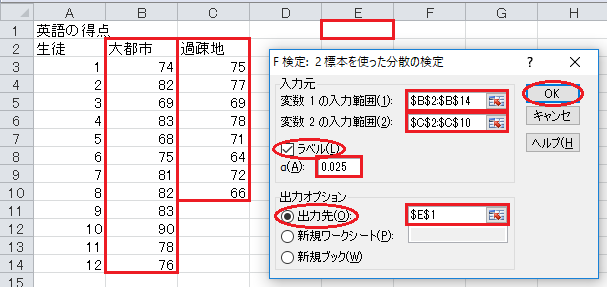
「P(F<=f) 片側」が p 値です。 ただし、この p 値は片側の確率なので、 p 値と0.025を比較するか、両側の p 値(2倍した値)と0.05を比較します。
注意: 分析ツールの F 検定の片側の p 値が0.5を超える場合、2倍して両側の p 値を求めると、1を超えてしまいます。 この場合は、1−片側の p 値、をあらためて片側の p 値にしてください。
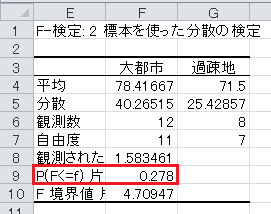
結論としては、両側の p 値が0.05以上なので、有意水準5%で有意ではなく、母分散が等しいという帰無仮説は棄却されず、母分散が等しくないという対立仮説も採択されません。 したがって、等分散を仮定します。
次に、等分散を仮定した t 検定を行います。 帰無仮説は英語の得点に差がないとし、対立仮説は英語の得点に差があるとします。 有意水準5%で両側検定を行います。
リボンの「データ」をクリックし、「データ分析」をクリックします。 すると、「データ分析」ウィンドウが開くので、「t 検定: 等分散を仮定した 2 標本による検定」をクリックして、「OK」ボタンをクリックします。
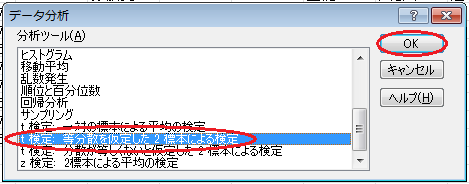
「変数 1 の入力範囲」に大都市のデータ$B$2:$B$14を入力し、「変数 2 の入力範囲」に過疎地のデータ$C$2:$C$10を入力します。 「仮説平均との差異」入力欄は空欄のままにし、「ラベル」チェックボックスをオンにし、「α」入力欄に0.05を入力します。 「出力オプション」の「出力先」をクリックし、空いているセル(例えば$E$12)を入力します。
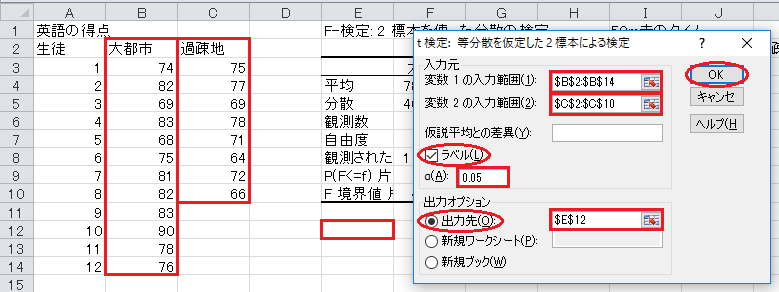
「P(T<=t) 両側」が p 値です。
結論としては、 p 値が0.05未満なので、有意水準5%で有意であり、英語の得点に差がないという帰無仮説は棄却され、英語の得点に差があるという対立仮説が採択されます。
検定の結果: 英語の得点に差があると言える。
表「50m走のタイム」は、大都市の中学生と過疎地の中学生との間で、50m走のタイムに差があるかどうかを標本調査したものです。
英語の得点と同様に、ドット・チャートを作成します。
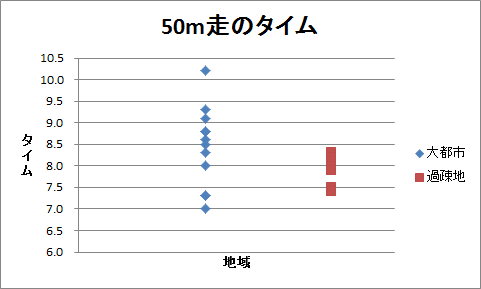
ドット・チャートを見ると、散らばりには差がありそうですが、平均には差がなさそうです。
表「50m走のタイム」についても、英語の得点と同様に、 F 検定で母分散が等しいかを確かめ、 t 検定で母平均の差を確かめます。
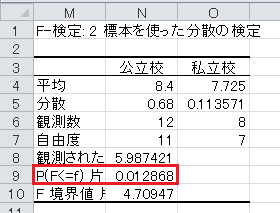
まずは F 検定です。 帰無仮説は母分散が等しいとし、対立仮説は母分散が等しくないとします。 有意水準5%で両側検定を行います。
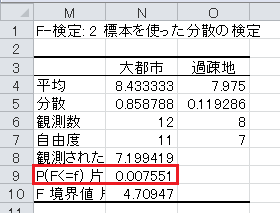
両側の(2倍した) p 値が0.05未満なので、有意水準5%で有意であり、母分散が等しいという帰無仮説は棄却され、母分散が等しくないという対立仮説が採択されます。 したがって、分散が等しくないと仮定します。
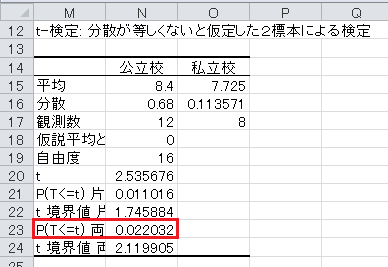
次は、分散が等しくないと仮定した t 検定です。 帰無仮説は50m走のタイムに差がないとし、対立仮説は50m走のタイムに差があるとします。 有意水準5%で両側検定を行います。
英語の得点と同じように t 検定を行うのですが、「t 検定: 分散が等しくないと仮定した 2 標本による検定」を利用します。
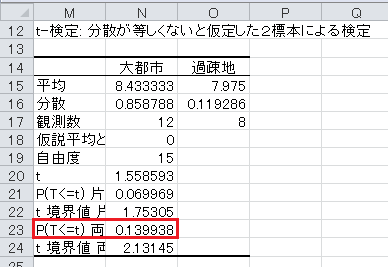
p 値が0.05以上なので、有意水準5%で有意ではなく、50m走のタイムに差がないという帰無仮説は棄却されず、50m走のタイムに差があるという対立仮説も採択されません。
検定の結果: 50m走のタイムに差があるとは言えない。
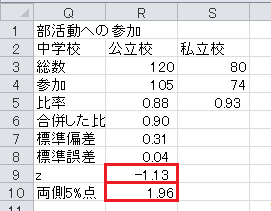
表「部活動への参加」は、大都市の中学生と過疎地の中学生との間で、部活動への参加率に差があるかどうかを標本調査したものです。 (比率のドット・チャートというものは、ありません。) 帰無仮説は部活動への参加率に差がないとし、対立仮説は部活動への参加率に差があるとします。 有意水準5%で両側検定を行います。 比率の検定( z 検定)については、Excelの関数で計算します。
まず、セルQ5から下に、「比率」、「合併した比率」、「標準偏差」、「標準誤差」、「z」、「両側5%点」と入力します。 両側5%点の1.96も入力しておきます。
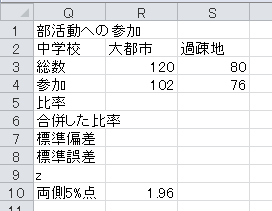
比率=参加/総数、です。
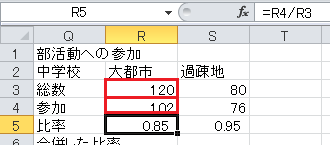
合併した比率=(総数1×比率1+総数2×比率2)/(総数1+総数2)、です。
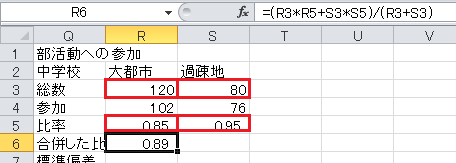
標準偏差=√(合併した比率×(1−合併した比率))、です。
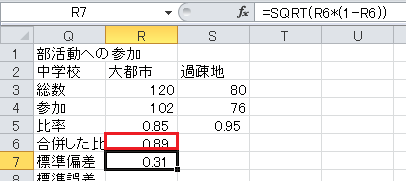
標準誤差=標準偏差×√(1/総数1+1/総数2)、です。
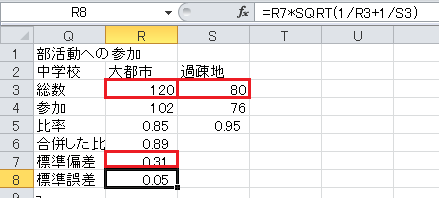
z=(比率1−比率2)/標準誤差、です。
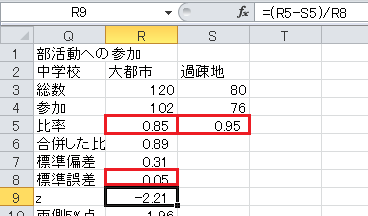
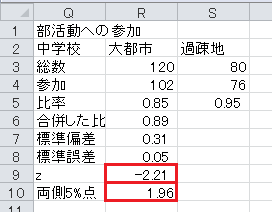
z 統計量(の絶対値)が両側5%点より大きいので、有意水準5%で有意であり、部活動への参加率に差がないという帰無仮説は棄却され、部活動への参加率に差があるという対立仮説が採択されます。
検定の結果: 部活動への参加率に差があると言える。
以下のファイルをダウンロードしてください。
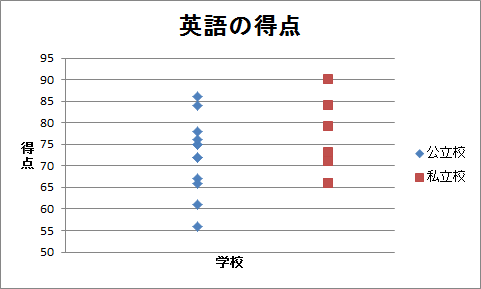
(1)表「英語の得点」は、公立校の中学生と私立校の中学生との間で、英語の得点に差があるかどうかを標本調査したものです。 このデータのドット・チャートを作成してください。
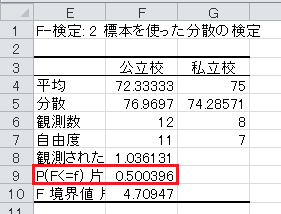
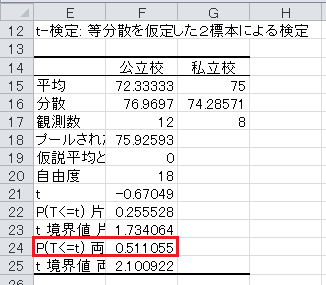
(2)表「英語の得点」について、帰無仮説は英語の得点に差がないとし、対立仮説は英語の得点に差があるとします。 有意水準5%で両側検定を行います。 F 検定を行ってから t 検定を行い、結果を答えてください。
(3)表「50m走のタイム」は、公立校の中学生と私立校の中学生との間で、50m走のタイムに差があるかどうかを標本調査したものです。 このデータのドット・チャートを作成してください。
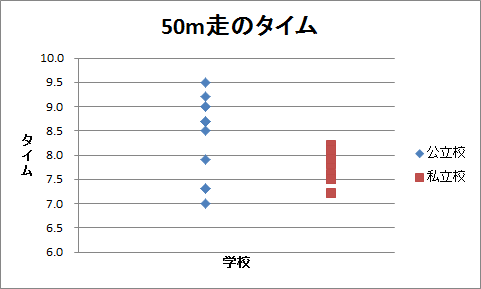
(4)表「50m走のタイム」について、帰無仮説は50m走のタイムに差がないとし、対立仮説は50m走のタイムに差があるとします。 有意水準5%で両側検定を行います。 F 検定を行ってから t 検定を行い、結果を答えてください。
(5)表「部活動への参加」は、公立校の中学生と私立校の中学生との間で、部活動への参加率に差があるかどうかを標本調査したものです。 帰無仮説は部活動への参加率に差がないとし、対立仮説は部活動への参加率に差があるとします。 有意水準5%で両側検定を行います。 z 検定を行い、結果を答えてください。
今日の演習10の答案(Excelファイルと検定の結果)をメールで提出してください。 差出人は学内のメール・アドレス(学生番号@cis.twcu.ac.jp)とし、宛先はkonishi@cis.twcu.ac.jpとします。 メールの本文には、学生番号、氏名、科目名、授業日(11月30日)を明記してください。
Excelの関数で、 F 検定の p 値だけは求めることができます。 関数の形式は、
FTEST(配列1,配列2)
です。
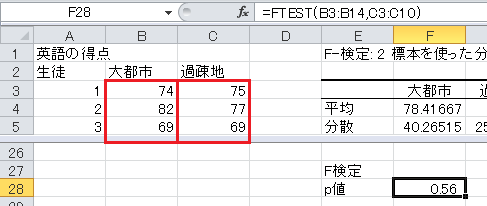
セルE28に「p値」と入力し、セルF28に=FTEST(B3:B14,C3:C10)と入力すると、 p 値0.56が得られます。
Excelの関数で、 t 検定の p 値だけは求めることができます。 関数の形式は、
TTEST(配列1,配列2,尾部,検定の種類)
です。 ここで、「尾部」は、片側検定なら1, 両側検定なら2です。 また、「検定の種類」は、対標本なら1, 等分散を仮定した2標本なら2, 分散が等しくないと仮定した2標本なら3です。
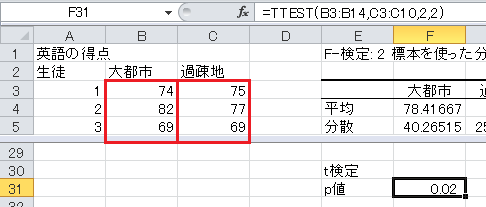
セルE31に「p値」と入力し、セルF31に=TTEST(B3:B14,C3:C10,2,2)と入力すると、 p 値0.02が得られます。