前回の授業では、20歳以上の日本人の身長のデータを利用しました。 実はこのデータ、日本人全員の身長を測定したわけではありません。 測定した人数は、男性3,022人、女性3,734人となっています。
調査の目的となる集団(全部)を 母集団 ( population )と呼びます。 そして、実際に調査する要素(一部)を 標本 ( sample )または サンプル と呼びます。 母集団から標本を選び出すことを、 標本抽出 ( sampling )または サンプリング と呼びます。
前回の授業の場合なら、20歳以上の日本人全員が母集団です。 そして、男性3千人余り、女性3千人余りが標本です。 本当は母集団(20歳以上の日本人全員)を調査したいけれど、それは時間的にも経済的にも不可能なので、代わりに標本(男性3千人余り、女性3千人余り)を調査したということです。
母集団の平均を 母平均 ( population mean )と呼び、母集団の分散を 母分散 ( population variance )と呼びます。 このように、母集団の統計的数量は母何とかと呼びます。 これに対して、標本の平均を 標本平均 ( sample mean )と呼び、標本の分散を 標本分散 ( sample variance )と呼びます。 このように、標本の統計的数量は標本何とかと呼びます。
記号で表すときは、母平均はμ、母分散はσ 2 で表します。 このように、母集団の場合にはギリシャ文字を使います。 これに対して、標本平均は X , 標本分散は s 2 で表します。 このように、標本の場合にはアルファベットを使います。
なお、分散には分母が n のものと n −1のものがありますが、標本分散 s 2 の場合は分母が n −1のものを使います。
統計的推測とは、一部(標本)から全部(母集団)を推測することでした。 母集団について最も推測したいのは、母集団の平均、すなわち母平均でしょう。 今日は、どのようにして標本から母平均を推測するかを考えます。 身長の例で言えば、数千人のデータから全国平均を推測しようということです。
取りあえず、標本の平均、すなわち標本平均 X を計算し、これがだいたい母平均μではないかと考えます。 この考え方自体はそれほど間違っていませんが、多少の 誤差 ( error ) X −μがあるでしょう。 標本を選び直してみると、標本平均は多少異なる値になるはずで、再び誤差が出るでしょう。 標本を何度も選び直したと仮定し、その都度得られた標本平均を集めると、その分布(確率分布)については、中心極限定理と呼ばれる定理が成り立ちます。
中心極限定理 ( central limit theorem ): 母平均μ、母分散σ 2 (母標準偏差σ)の母集団から大きさ n の標本を抽出すると、標本平均 X の確率分布は、平均μ、標準偏差σ/√ n の正規分布となる。
この定理から、母平均μに対する標本平均 X の誤差 X −μの確率分布は、平均0, 標準偏差σ/√ n の正規分布となります。 この誤差の標準偏差
を 標準誤差 ( standard error )と呼び、s.e.などと書きます。
標準誤差の式から、次のことが言えます。
標本をたくさん取れば誤差が減るだろうという直感は正しいのですが、標本を100倍にして、やっと誤差が10分の1になるのです。
推定 ( estimation )とは、標本から母集団の統計的数量を推測することです。 今日の目標である、標本から母平均を推測することも、推定の一つです。
母集団の統計的数量をズバリ言い当てることは難しいので、ある程度の幅を持って推定することにします。 これを 区間推定 ( interval estimation )といいます。 区間推定では確率を用います。 例えば、95%の確率でこの区間に入るということです。
区間推定における確率を 信頼度 ( confidence level )と呼び、区間を 信頼区間 ( confidence interval )と呼びます。 以後、 a 以上 b 以下という区間を、[ a , b ]と書くことにします。
ここで、正規分布の両側5%点を思い出してください。 正規分布では、平均のプラスマイナス1.960×標準偏差、の範囲に95%のデータが入るということでした。 これと中心極限定理を組み合わせると、誤差 X −μは95%の確率で区間
に入るので、母平均μは95%の確率で区間
に入ることになります。 これを区間推定の言葉で言えば、母平均μは信頼度95%で信頼区間
に入るということです。 つまり、 X −1.960×σ/√ n 以上 X +1.960×σ/√ n 以下と推定されるということです。
上記の通りに区間推定を行いたいのですが、母標準偏差σが分からないと計算できません。 これについては、以下のようにします。
ここで、 t分布 ( t-distribution )とは、標準正規分布を補正した分布で、標本が小さい場合に用いられます。 t 分布は、 自由度 ( degree of freedom )と呼ばれるパラメータを持ちます。 ここでは、
だと思ってください。
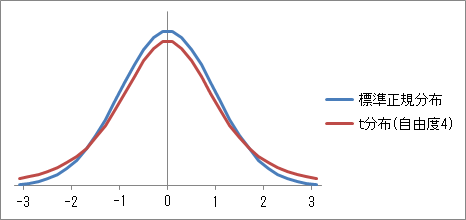
以下は、 t 分布の概形です。 標準正規分布と似ていることに注意してください。

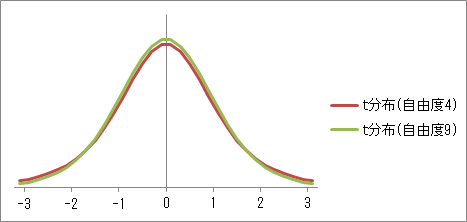
t 分布は、自由度が変わると、確率密度も変わります。 自由度が大きくなるほど、 t 分布は標準正規分布に近づくことが知られています。
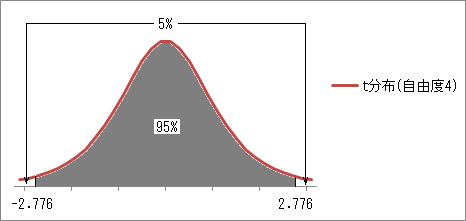
t 分布の両側5%点は、1.960より少し大きくなります。 例えば、自由度4の t 分布の両側5%点は、2.776です。 この値は、Excelや「Rコマンダー」で計算できますので、以下の操作を参照してください。
参考までに、いくつかの自由度の t 分布の両側5%点と上側5%点を載せておきます。
| 標本の大きさ | 5 | 10 | 15 | 20 | 25 | 30 | ... |
大きい
(正規分布) |
|---|---|---|---|---|---|---|---|---|
| 自由度 | 4 | 9 | 14 | 19 | 24 | 29 | ... | |
| 両側5%点 | 2.776 | 2.262 | 2.145 | 2.093 | 2.064 | 2.045 | ... | 1.960 |
| 上側5%点 | 2.132 | 1.833 | 1.761 | 1.729 | 1.711 | 1.699 | ... | 1.645 |
それでは、20歳以上の日本人の平均身長を区間推定しましょう。 標本は大きいので、母標準偏差σの代わりに標本標準偏差 s を用い、
を計算します。
男性の場合は、標本の大きさ n =3,022, 標本平均 X =166.6, 標本標準偏差 s =7.2なので、
となり、日本全国の平均は、信頼度95%で166.3cm以上166.9cm以下と推定されます。
女性の場合は、標本の大きさ n =3,734, 標本平均 X =153.4, 標本標準偏差 s =7.1なので、
となり、日本全国の平均は、信頼度95%で153.2cm以上153.6cm以下と推定されます。
標本が小さい場合、母標準偏差σの代わりに標本標準偏差 s を用い、さらに、正規分布の両側5%点の1.960の代わりに t 分布の両側5%点を用います。 例えば、標本の大きさが5ならば、自由度は5−1=4なので、両側5%点は2.776となり、
を計算することになります。
具体例は、以下のExcelによる計算を見てください。
比率とは、例えばある議題に100人中60人が賛成したら、賛成の比率は0.60です。 比率についても区間推定が可能です。 すなわち、100人中60人賛成する議題は、日本全国ではどのぐらい賛成するのかということです。
簡単に言うと、標本比率 p に対して、標本平均を p , 標本標準偏差を√( p ×(1− p ))として、標本が大きな場合の方法で区間推定ができます。 つまり、
の X を p に読み替え、 s を√( p ×(1− p ))に読み替えた、
となります。
100人中60人が賛成した場合、標本の大きさ n =100, 標本比率 p =0.60なので、
となり、信頼度95%で、日本全国で50%以上70%以下が賛成すると推定されます。
100人という人数に賛成反対を聞いて、誤差が10%もあるのは大きいと感じるかもしれません。 もちろん、より大人数に聞けば誤差は減ります。 1,000人中600人が賛成した場合、信頼度95%の信頼区間は[0.57, 0.63]です。 10,000人中6,000人が賛成した場合、信頼度95%の信頼区間は[0.59, 0.61]です。
t 分布の両側5%点は、ExcelのTINV関数で計算できます。 ( t 分布の逆関数(inverse)という意味です。) 確率 p , 自由度 f に対して、
TINV( p , f )
で、自由度 f の t 分布の両側100 p %点が計算されます。
試しに、Excelを起動して、新しいウィンドウのセルA1に
=TINV(0.05,4)
と入力すると、2.776...と表示されます。

それでは、Excelを利用して、信頼区間(Excelでは誤差範囲と言います)を計算しましょう。 ある業者が、全国の小学五年生に対して学力試験を行う予定とします。 同時に、科目の好き嫌いに関するアンケートも予定しているとします。 その準備として、16人に国語の試験、8人に算数の試験を行いました。 また、160人に国語が好きか、80人に算数が好きかを聞きました。 次のExcelファイルをダウンロードしてください。
まず、セルA19から、「標本の大きさ」、「平均」、「標準偏差」、「標準誤差」、「自由度」、「両側5%点」、「誤差95%」、「下限95%」、「上限95%」と入力します。
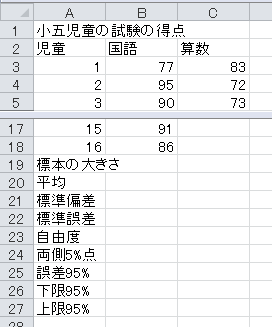
標本の大きさは、ExcelのCOUNT関数で求められます。 COUNT関数は、データが入っているセルの個数を数えます。 セルB19に数式=COUNT(B3:B18)と入力してください。
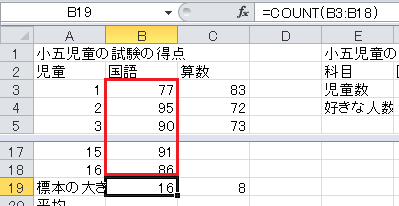
平均は、ExcelのAVERAGE関数で求められます。 セルB20に=AVERAGE(B3:B18)と入力してください。 範囲に空のセルがあると読み飛ばしますので、そのままセルC20にコピー・アンド・ペーストできます。
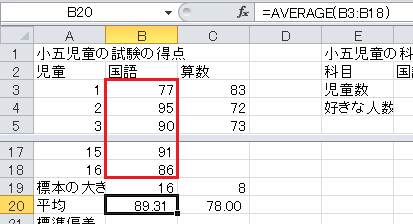
標準偏差は、ExcelのSTDEV関数で求められます。 標本なので、分母が n −1のものを使います。 セルB21に=STDEV(B3:B18)と入力してください。 範囲に空のセルがあると読み飛ばしますので、そのままセルC21にコピー・アンド・ペーストできます。
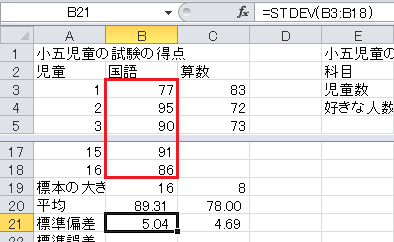
標準誤差は、標準偏差/√標本の大きさ、なので、セルB22に=B21/SQRT(B19)と入力してください。 ここで、SQRTとは平方根(square root)を求める関数です。
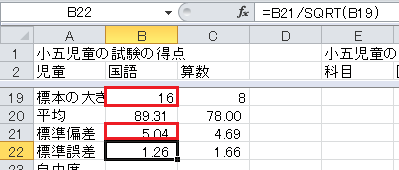
自由度は、標本の大きさ−1なので、セルB23に=B19-1と入力してください。
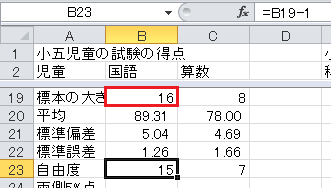
t 分布の両側5%点は、Excelの関数でTINV(0.05,自由度)で求められます。 セルB24に=TINV(0.05,B23)と入力してください。
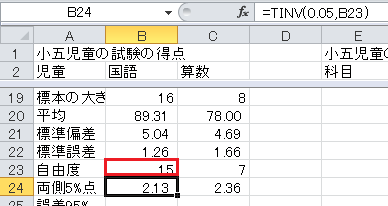
信頼度95%の誤差は、標準誤差×両側5%点、です。 セルB25に=B22*B24と入力してください。
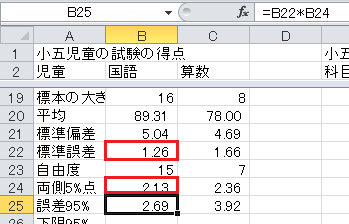
信頼度95%の信頼区間の下限は、標本平均−信頼度95%の誤差、です。 セルB26に=B20-B25と入力してください。
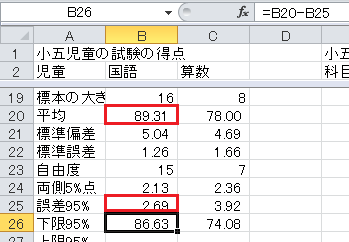
信頼度95%の信頼区間の上限は、標本平均+信頼度95%の誤差、です。 セルB27に=B20+B25と入力してください。
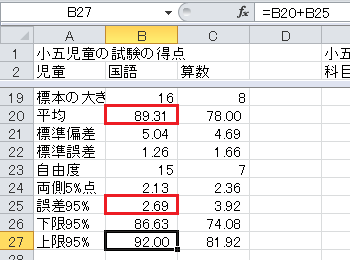
これで信頼区間(誤差範囲)の表が完成しました。
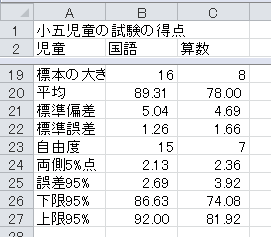
次に、棒グラフを作成し、この信頼区間(誤差範囲)を棒グラフに付けましょう。
まず、セルA2からC2とA20からC20をドラッグするのですが、離れたセルについては、commandキー(Windowsの場合はCtrlキー)を押しながらドラッグします。
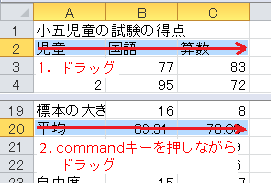
リボンの「グラフ」(Windowsの場合は「挿入」)をクリックし、「グラフの挿入」項目で「縦棒」→「集合縦棒」とクリックします。 すると、棒グラフが表示されます。
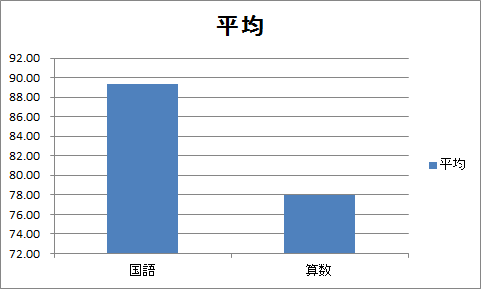
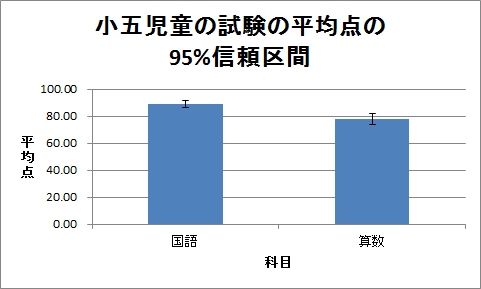
上側のグラフ・タイトルをダブル・クリックし、「小五児童の試験の平均点の95%信頼区間」に変更します。 右側の凡例「平均」をクリックし、deleteキーを押して削除します。
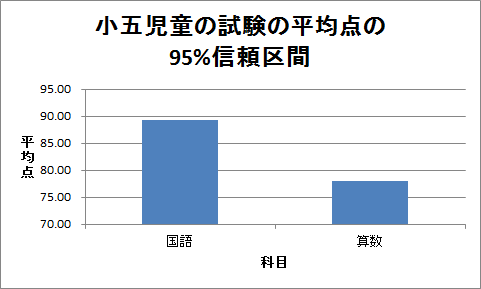
リボンの「グラフ レイアウト」をクリックし、「ラベル」項目で「軸ラベル」→「横軸ラベル」→「軸ラベルを軸の下に配置」とクリックし、軸ラベルを「科目」に変更します。 「ラベル」項目で「軸ラベル」→「縦軸ラベル」→「軸ラベルを垂直に配置」とクリックし、軸ラベルを「平均点」に変更します。
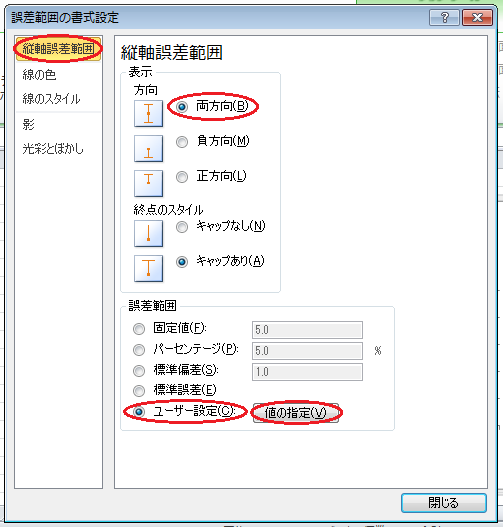
リボンの「グラフ レイアウト」をクリックし、「解析」項目(Windowsの場合は「分析」項目)で「誤差範囲」→「誤差範囲のオプション」とクリックします。 すると、「誤差範囲の書式設定」ウィンドウが開くので、「誤差範囲」タブをクリックし、「両方向」アイコンをクリックし、「ユーザー設定」ラジオ・ボタンをオンにし、「値の指定」ボタンをクリックします。
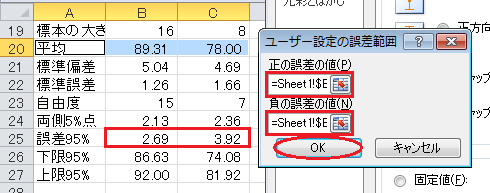
すると、「ユーザ設定の誤差範囲」ウィンドウが開くので、「正の誤差の値」入力欄と「負の誤差の値」入力欄に、95%信頼区間の誤差(セルB25からC25まで)を入力します。
これで、信頼区間(誤差範囲)付きの棒グラフが完成します。
母比率の信頼区間の計算も、本質的には母平均の場合と同じです。
まず、必要な項目を入力します。 両側5%点の1.960も入力します。
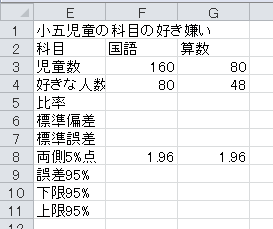
「比率」は、好きな人数/児童数、です。
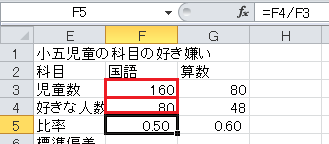
「標準偏差」は、√(比率×(1−比率))、です。
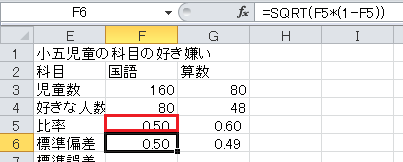
「標準誤差」は、標準偏差/√児童数、です。
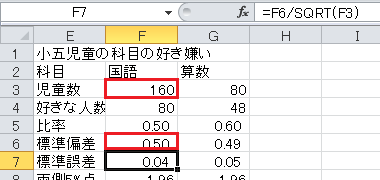
「誤差95%」は、標準誤差×1.960、です。
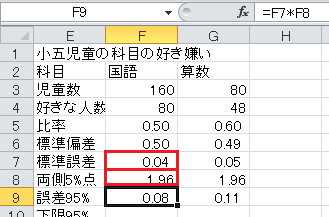
「下限95%」は、比率−誤差95%、です。
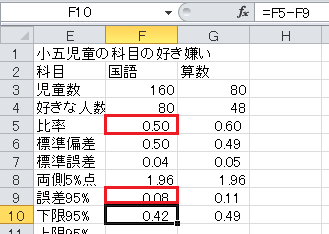
「上限95%」は、比率+誤差95%、です。
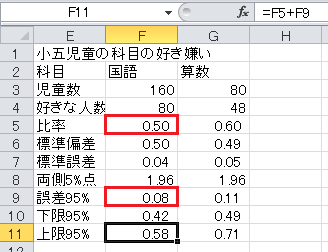
これで信頼区間(誤差範囲)の表が完成しました。
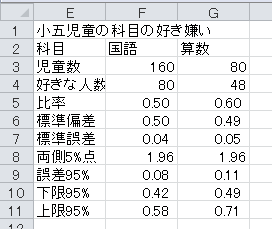
信頼区間(誤差範囲)付きの棒グラフも、同じように作成できます。
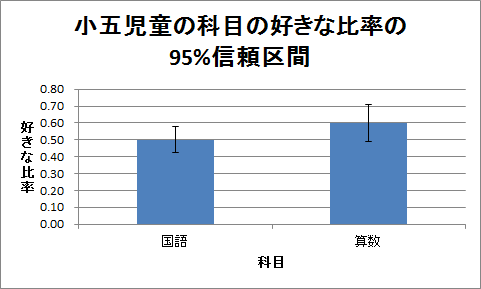
「分析ツール」を利用すると、信頼区間の誤差が求められます。
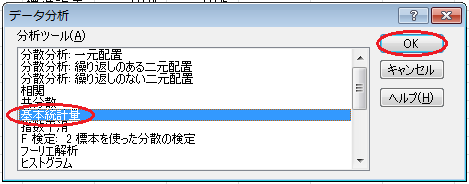
リボンの「データ」をクリックし、「分析」項目の「データ分析」をクリックします。 すると、「データ分析」ウィンドウが開くので、「基本統計量」をクリックし、「OK」ボタンをクリックします。
すると、「基本統計量」ウィンドウが開くので、「入力範囲」入力欄にデータの範囲(セルB2からC18まで)を入力し、「列」ラジオ・ボタンをオンにし、「先頭行をラベルとして使用」チェックボックスをオンにし、「出力先」ラジオ・ボタンをオンにし、その入力欄に余白(セルA29)を入力し、「平均の信頼区間の出力」チェックボックスをオンにし、その入力欄に「95」を入力して、「OK」ボタンをクリックします。
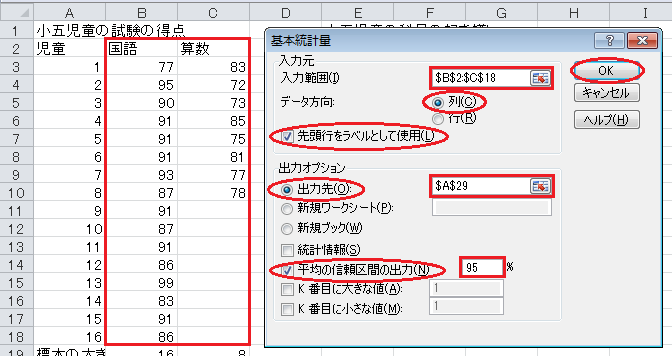
すると、指定された出力先に、信頼区間の誤差が表示されます。
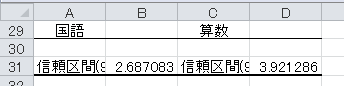
「StatPlus」を利用すると、信頼区間そのものが求められます。
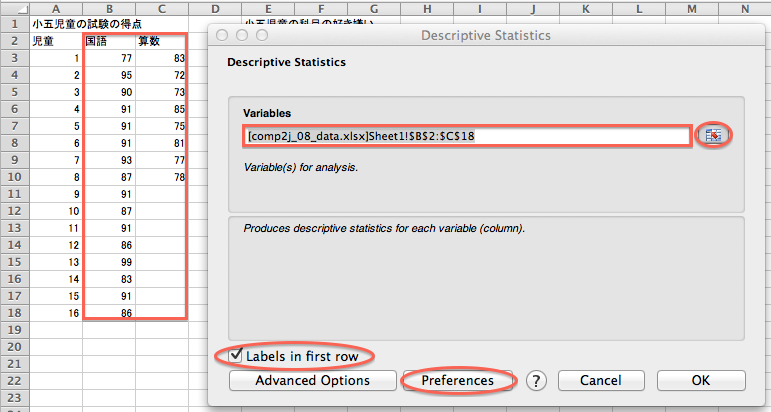
「StatPlus」を起動し、メニューバーで「Statistics」→「Basic Statistics and Tables」→「Descriptive Statistics」とクリックします。 すると、「Descriptive Statistics」ウィンドウが開くので、「Variables」入力欄の右のボタンをクリックし、Excelのデータの範囲(セルB2からC18まで)をドラッグし、「Descriptive Statistics」ウィンドウをクリックします。 そして、「Labels in first row」チェックボックスをオンにして、「Preferences」ボタンをクリックします。
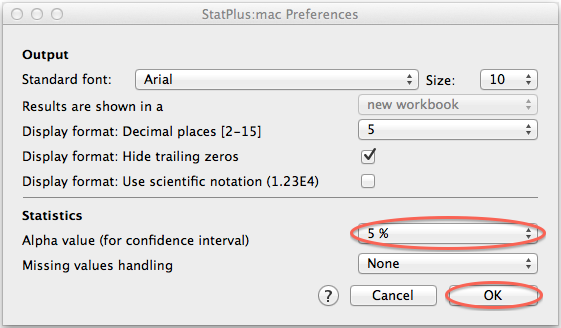
すると、「Preferences」ウィンドウが開くので、「Alpha value (for confidence interval)」メニューを「5%」に設定して、「OK」ボタンをクリックします。
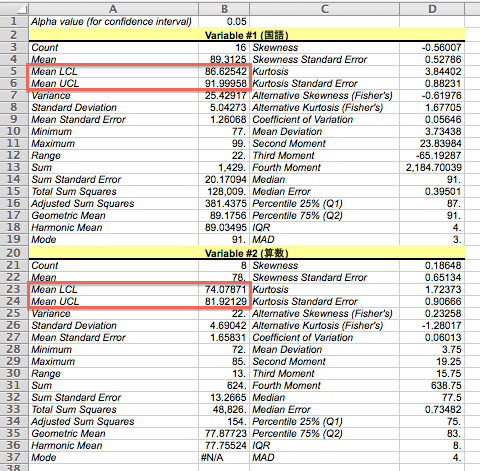
最後に、「Descriptive Statistics」ウィンドウの「OK」ボタンをクリックします。 すると、新しくExcelのウィンドウが開き、この「Mean LCL」という項目に95%信頼区間の下限、「Mean UCL」という項目に95%信頼区間の上限が表示されます。 (LCLは下側信頼限界(lower confidence limit)、UCLは上側信頼限界(upper confidence limit)です。)
まず、「Rコマンダー」で、 t 分布の両側5%点を求めます。
「Rコマンダー」を起動し、「Rコマンダー」ウィンドウで、「分布」→「連続分布」→「t分布」→「t分布の分位点」とクリックします。 すると、「t分布の分位点」ウィンドウが開くので、「確率」入力欄には、両側5%点なら上側2.5%点なので、その下側の確率0.975を入力し、「自由度」入力欄に自由度を入力し、「下側確率」ラジオ・ボタンをオンにして、「OK」ボタンをクリックします。
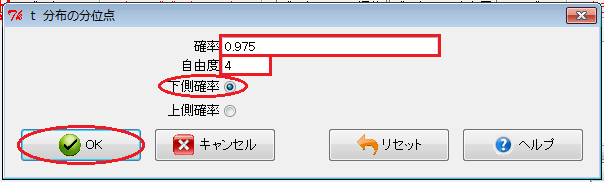
すると、「出力ウィンドウ」欄に、 t 分布の両側5%点が表示されます。
「Rコマンダー」を利用すると、信頼区間を直接グラフで表すことができます。 もし、信頼区間の数値が必要なら、次回以降説明する検定を行えば表示されます。
まず、適宜コピー・アンド・ペーストして、Excelのデータを以下のような形式に変更します。 (Japaneseは国語、arithmeticは算数。)
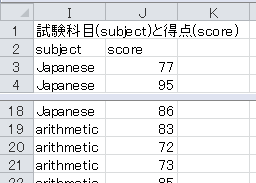
このデータを「Rコマンダー」にインポートし、「Rコマンダー」ウィンドウで「グラフ」→「平均のプロット」とクリックします。 すると、「平均のプロット」ウィンドウが開くので、「因子」欄の「subject」をクリックし、「目的変数」欄の「score」をクリックし、「信頼区間」ラジオ・ボタンをオンにし、「信頼水準」入力欄に「0.95」と入力して、「OK」ボタンをクリックします。
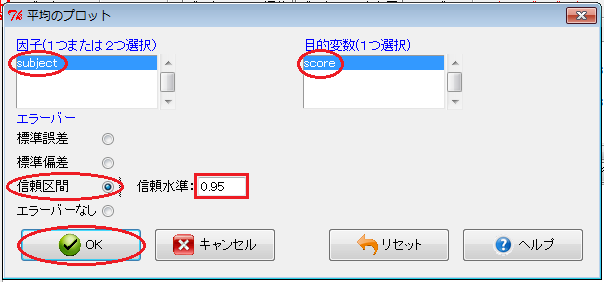
すると、信頼区間付きの折れ線グラフが表示されます。
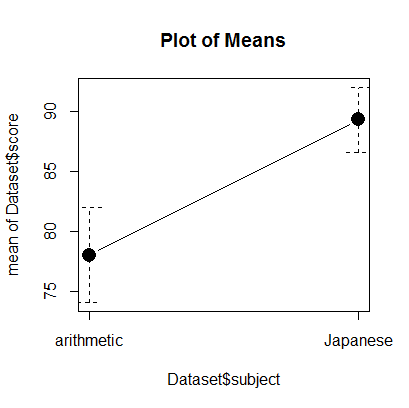
ある業者が、全国の中学二年生に対して学力試験を行う予定とします。 同時に、科目の好き嫌いに関するアンケートも予定しているとします。 その準備として、20人に英語の試験、14人に数学の試験、10人に国語の試験を行いました。 また、200人に英語が好きか、140人に数学が好きか、100人に国語が好きかを聞きました。 このデータをまとめたExcelファイルをダウンロードしてください。
(1)信頼度95%で、全国での試験の平均点の信頼区間(誤差範囲)を求めてください。 標本は小さいと考えてください。
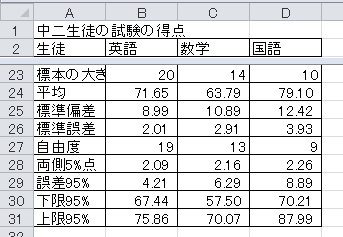
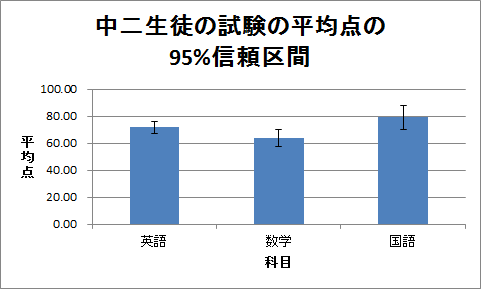
(2)この信頼区間(誤差範囲)が付いた棒グラフを作成してください。
(3)信頼度95%で、全国での科目の好きな比率の信頼区間(誤差範囲)を求めてください。
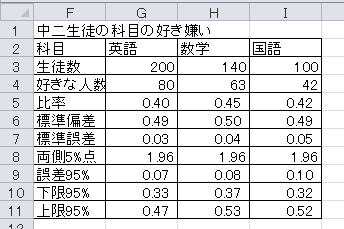
(4)この信頼区間(誤差範囲)が付いた棒グラフを作成してください。
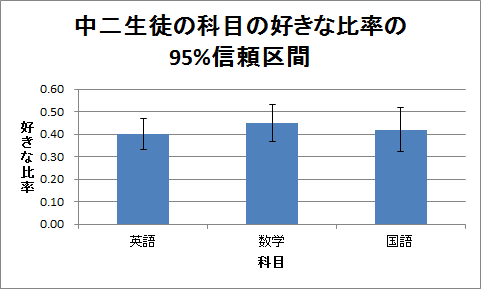
今日の演習8の答案(Excelファイル)をメールで提出してください。 差出人は学内のメール・アドレス(k12x1001@cis.twcu.ac.jpなど)とし、宛先はkonishi@cis.twcu.ac.jpとします。 メールの本文には、学生番号、氏名、科目名、授業日(11月27日)を明記してください。