巡回セールスマン問題

巡回セールスマン問題(Traveling salesman problem:TSP)とは、あるセールスマン が、いくつかの都市を順番に一度ずつ訪問し、最後に出発点に戻って来るときに 最短の距離で各都市を訪問するための順路を決定する問題である。 訪問すべき都市の数を N とすると、すべての組合せ数は になるので訪問すべき都市数が増加すると極端に難しい問題とな る。

いま A,B,C,D,E の 5 都市を訪問する TSP を考える。まず都市の数の 2 乗 25 個のニューロンを用意する。行方向に都市、列方向に訪問順序をとるとすれ ば、

のような表は BACED の順序で都市を訪問することを表している。 X 行 i 列のニューロンの出力を と表し、都市 X と 都市 Y との 距離を と表すことにすると、

1. 同じ都市を２度訪問しない条件(同一行に 1 は一つしかない)

   

2. 同時に２都市を訪問できない条件(同一列に 1 は一つだけ)

   

3. 全ての都市を訪問する条件(すべての 1 を足し合わせると都市数に一致 する)

   

という条件のもとで、次の目的関数(経路の総距離にあたる)

を最小にする問題となる。エネルギー関数は、これらの制約条件のもとで 目的関数を最小にする制約付最小化の問題になる。

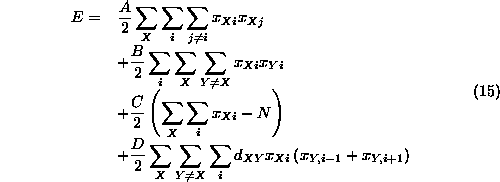
ホップフィールドは A=B=500, C=200, D=500, N=15 として 計算している。

と比較すれば、

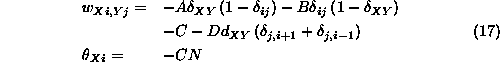
となる。ここで はクロネッカーのデルタ

である。 実際に programing するときには

を十分に小さい , で近似して

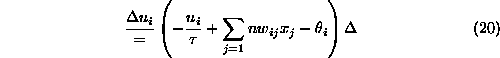
という近似差分を用いて を

の漸化式で更新すればよい。