誤差逆伝播法(一般化デルタルール)

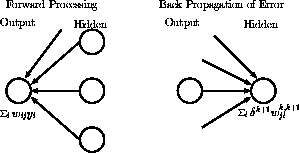
XOR 問題でも見たように、パーセプトロンの問題点は学習が出力層と 中間層の間だけで行われ、下の層に伝播しないことです。 この点を改良したのがバックプロパゲーション(一般化デルタルール)と 呼ばれるものです。

m 層のネットワークを考え、k 層の i 番目の ニューロンへの総入力を , このニューロンの出力を , k-1 層の i 番目のニューロンから k 層の j 番目のニューロンへの結合係数を と表記します。 各ニューロンの出力は

 

で定義されているものとします。 あるデータ と教師信号 が与えられたとき 教師信号と出力との 2 乗誤差を

とします。 この誤差関数 E は、教師信号と出力層とが異なれば異なるほど 大きくなるので、 E が減少する方向に の値を逐次更新していくこと ことを考えます。

 

式(16)は最急降下法と呼ばれる最適化問題を解く手法の一つです。 関数は は と の関数ですが、 さらに は の関数で、 さらにさらに は の関数ですから合成関数の微分公式により

 

となります。もし仮に(13)式で与えられている 出力関数が線形関数 y(x)=x であれば、(20)式は となってパーセプトロンの学習式 と一致します。

次に中間層以下第 n 層( )のニューロン の結合係数の更新には、

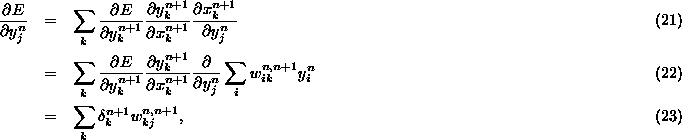
を誤差信号 として再帰的に計算します。 以上をまとめると、結合係数の修正量 は

 

となります。式(25)を見ると誤差の計算がデータ処理とちょうど逆の 流れで入力層まで伝播するようになっています。これが誤差逆伝播法の由来です。