パーセプトロンの情報処理能力

パーセプトロンの収束定理:

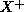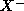と が線形分離可能であるならばパーセプトロンの学習は有限回で 停止し、そのとき得られた結合(係数は)すべての入力パターンに対して正解を与 えるものになっている。

パーセプトロンの循環定理:

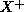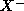と が線形分離可能でない場合、パーセプトロンは、一般に収束しないが 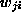の大きさは有界であり有限個の結合状態を循環する。

パーセプトロンの群不変定理:

ある変換群のもとで幾何学的な性質を判断するパーセプトロンに、 その変換群のもとで同値な 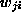を使うことで同値な値に対して 同じ出力を得ることができる。

その他の研究者による証明には次のようなものもあります。

論理関数の計算に関する完全性:

それぞれのユニットがしきい素子である三層のネットワークによって、中間 層のユニットを必要なだけたくさん使えば、任意の2値論理関数を実現でき る。

いかに複雑な関数であっても絶対可積分であれば2層のパーセプトロン で実現できる:

Irie and Miyake, (1988), ``Capabilities of Three-layered Perceptrons'', Proc. IEEE International Conference on Neural Networks, Vol.1, P.641-648.

連続関数のシミュレータとしての完全性(船橋, 1988):

それぞれのユニットがジグモイド状の関数である4層ネットワークによって、 中間層のユニットを必要なだけたくさんつかえば、ユニット間の結合(およ びジグモイド状関数のしきい値)を適切に設定することによって、任意の連 続な関数 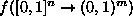を任意の精度で近似すること ができる