連絡事項#

来週 6月7日と再来週 6 月 14 日は休講
期末試験は駒澤大学の試験スケジュールの中で行います
すべて持ち込み可。ただし人間の持ち込みは不可。
今回の資料の PDF ファイル

予定再考#

4月12日 ~~イントロダクション，人工知能の歴史，計算論的神経科学 vs. 認知科学 vs. 人工知能~~
4月19日 ~~生理学的背景~~，~~ニューラルネットワーク~~，情報理論，サイバネティックス
4月26日 ~~機械学習概論~~
5月10日休講
5月17日 ~~パターン認識~~，~~パーセプトロン~~，パンデモニアム，~~文字認識，画像認識~~
5月24日 ~~一般画像認識~~，~~顔認識~~，動画認識，意味的画像分節化，~~畳込みニューラルネットワーク~~
5月31日 ~~誤差逆伝播法，多層化の工夫，内部表象，表現学習~~，次元圧縮
6月07日休講
6月14日休講
6月21日 ~~脳のモデル~~，作動記憶，手続き記憶
6月28日リカレントニューラルネットワーク，自然言語処理，系列予測，自動翻訳，文章要約
7月05日単語，文章埋め込みモデルによる意味論
7月12日強化学習, ゲームAI，経済学，予測報酬誤差
7月19日画像認識と自然言語処理との融合，質疑応答生成，転移学習，マルチタスク学習
補講: メタ認知，メタ学習，ハイパーパラメータの自動調整
補講: 世界知識，メンタルモデル，メンタルシミュレーション
補講: 精神医学(統合失調症，強迫神経症，依存症，幻覚幻聴)，神経心理学(意味痴呆，相貌失認，失語，失行)
ReLU, tanh に触れていない
memo: バッチ正則化をやっていない
本日の次元圧縮でも，SGD, dropout と同じく

セルフリッジ Selfridge のパンデモニウム pandemonium モデル#

セルフリッジ (1958) ``Mechanisation of Thought Processes'' より

復習を兼ねてもう一度歴史#

LeNet5 (LeCun, 1998)#

LeCun (1998) より

AlexNet (Krizensky, et al., 2012)#

Krzensky et al (2012) より

GooLeNet (Inception) (Szegedy et. al, 2014)#

空間ピラミッド (2015) より

R-CNN (2015)#

Girshick (2013) より

残渣ネット (He et. al, 2015)#

He (2015) より

Fast R-CNN と Faster R-CNN (2014)#

Fast R-CNN

Faster R-CNN

セマンティックセグメンテーションとインスタンスセグメンテーション#

完全畳み込みネットワーク(Fully Convolutional Network:FCN) と呼ばれるセマンティックセグメンテーションを実現するネットワーク
FCN とは文字通り全ての層が畳込み層であるモデル

Long (2017) FCN

通常のCNN は，出力層のユニット数が識別すべきカテゴリー数であった。一方 FCN では入力画像の画素数だけ出力層が必要になる。
すなわち各画素がそれぞれどのカテゴリーに属するのかを出力する必要があるため出力層には，縦画素数 $\times$ 横画素数 $\times$ カテゴリー数の出力ニューロンが用意される。
図では，識別すべきカテゴリー数が 20 であったたま，どのカテゴリーにも属さない，すなわち背景を指示するもう1 つのカテゴリーを加えた計 21 カテゴリーの分類を行うことになる。
CNN では畳込演算によって畳込みのカーネル幅(受容野) だけ近傍の入力刺激を加えて計算することになるため，上位層では下位層に比べて受容野が大きくなることの影響で画像サイズは小さく(あるいは粗く) なってしまう
このため，最終出力層に入力層と同じ解像度の画素数を得るためには，畳込みと反対方向の解像度を細かくする工夫が必要となる。
これを解決する一つの方法がアンサンプリング(unsampling) と呼ばれる方法
下位のプーリング層の情報を用いて詳細な解像度を得る
図はアンサンプリングにより詳細な画像，すなわち最終的には入力画像と等解像度の出力を得る仕組みを示している。

同様の仕組みがセグネット Segnet でも取り入れられている

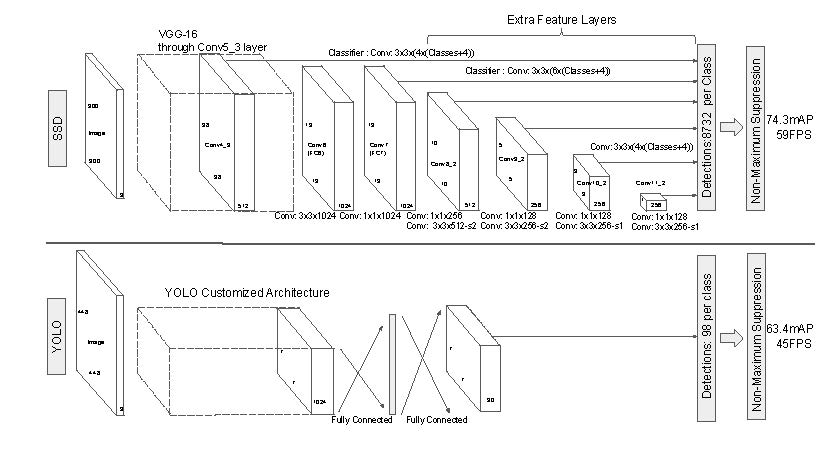
— You Only Look Once: Unified, Real-Time Object Detection, 2015.

A single neural network predicts bounding boxes and class probabilities directly from full images in one evaluation. Since the whole detection pipeline is a single network, it can be optimized end-to-end directly on detection performance.

画像変換#

まんがの画風変換#

``CartoonGAN: Generative Adversarial Networks for Photo Cartoonization'' CVPR 2018 (Conference on Computer Vision and Pattern Recognition)

左: 君の名は。右: 風の谷のナウシカ，より

Realtime Multi-Person 2D Human Pose Estimation using Part Affinity Fields, CVPR 2017 Oral

Paper: https://arxiv.org/pdf/1808.07371.pdf
Web site: https://carolineec.github.io/everybody_dance_now/

Winograd barrier (1972) 複雑さの障壁#

Winograd (1972) 曰く:

自然言語を理解するための SHRDLU プログラムのような大きなプログラムは、AI プログラミングのある種の行き止まりであると言われている。プログラムは各要素間の複雑な相互作用に対処しなければならず、同時にそれらを理解し，拡張するには大きな障害がある。どんな部分でも把握するためには、それが他の部分とどのように適合し、密な質量を示し、容易な足場がないかを理解する必要がある。プログラムを書いたとしても、すぐに頭に入れておくことができる限界に近づいている。

記号処理的，ルールベースアプローチの限界
Sutton の Bitter Lessons

次元削減，次元圧縮 dimensionality reduction#

Van der Maaten のページによれば次元圧縮 dimensionality reduction には 34 種類の方法があります。PCA, FA, MDS などが心理学では伝統的~~無批判~~に使われてきました。多くの心理学者は因子分析を好む ~~因子分析偏愛者，因子分析フェチ，factor analysis-pheria~~ ようですが，そのことを支持する理論的根拠は存在しません

PCA#

主成分分析 PCA: principal component analysis は一番最初に提案された手法で，固有値分解 に基づきます。
特に 2 次元へのマッピングは皮質地図 cortial map との対応が考えられるので興味深い
条件付き最大値を求める一般的方法でラグランジアン Lagrangian，あるいはラグランジェの未定乗数法 Lagrange multiplier が定義される。

最初は知らない方が良い知らなくても良いラグランジアンの説明#

$\begin{equation} \mathcal{L}=\mathbf{w}^\top\mathbf{X}^\top\mathbf{Xw}+\lambda\left({\mathbf{ww}^\top-1}\right) \end{equation}$

import numpy as np
import math

math.gamma(1)
math.gamma(2)
math.gamma(3)

t-SNE#

t-SNE は「ティーズニー」と発音します。
- ちなみに $f(x)$ はどのように発音するか知っていますか？あるいは $f\left(x\vert y\right)$ は？
心理学者以外では支配的(かも)
t: ** $t$ -分布
S: Stochastic 確率的
N: Neigbor 隣接(隣人)
E: Embedding 埋め込み
PCA, FA, 古典的 MDS (Torgerson) が固有値に基づくのに対して，t-SNE は多次元空間と低次元空有間への写像について確率的な仮定を考え，両者の分布が近づくように学習を行う。
- ここで，2 つの分布の距離を考える。距離の定義には様々が提案がなされているが カルバック=ライブラー ダイバージェンス(あるいは KL 距離)が用いられる。本日の付録参照
以下は van der Maaten and Hinton (2008) のオリジナル論文に掲載された結果である

van der Maaten and Hinton (2008) Fig.2

van der Maaten and Hinton (2008) Fig.3

t 分布( $\nu=1$ )と標準正規分布の確率密度分布 pdf

PCA と t-SNE の比較実験
スチューデントの $t$ 分布 $t$ 分布の確率密度関数 pdf は以下のとおり: 数学愛好者~~数学恐怖症 For all math-phobia~~の皆様へ

$\begin{equation} p(x,\nu)=\frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi}\,\Gamma\left(\frac{\nu}{2}\right)}\left(1+\frac{x^2}{\nu}\right)^{-\frac{\nu+1}{2}}. \end{equation}$

おそろしい形をしていますが，ポイントは $\Gamma$ 関数(がんまかんすう)であり，内部で使われている $\nu$ (「にゅう」と読むギリシャアルファベット)は自由でデータ数 $-1$ です。
$\Gamma$ はガンマ関数であり，階乗の連続量への拡張とみなすことができます。
最も簡単な場合 $\nu=1$ を考えれば，上式は以下のようになります。

$\begin{equation} p(x,\nu=1)=\frac{\Gamma\left(1\right)}{\sqrt{\nu\pi}\,\Gamma\left(\frac{1}{2}\right)}\left(1+x^2\right)^{-1}. \end{equation}$

さらに $\Gamma(1)=1$ , $\displaystyle\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}$ を考慮すれば，以下の式を得ます。

$\begin{equation} p(x,\nu=1)=\frac{1}{\pi}\frac{1}{1+x^2}, \end{equation}$

$\pi$ は円周率で定数ですから，グラフの形を考えるときには無視して構いません。従って $t$ 分布の本質は $\displaystyle\frac{1}{1+x^2}$ であることになります。
codolab で確認してみましょう。

import numpy as np
import math

print(math.gamma(1/2))

for i in range(1,11):
    print(i, math.gamma(i))

math.sqrt(math.pi) == math.gamma(1/2)

ガンマ関数の概形を描いてみましょう

import matplotlib.pyplot as plt
x = np.linspace(0.25,4)
y = [math.gamma(xi) for xi in x] 
plt.plot(x,y)

つづいて正規分布と $t$ -分布とを比較してみましょう

from scipy.stats import norm

x = np.linspace(norm.ppf(0.001), norm.ppf(0.999), 100)
nu = 1

plt.plot(x, t.pdf(x, nu), 'b-', lw=2, label='t')
plt.plot(x, norm.pdf(x),  'r-', lw=2, label='norm')
plt.legend()

用語集#

非線形性#

ReLU
Sigmoid
Tanh
GRU
LSTM

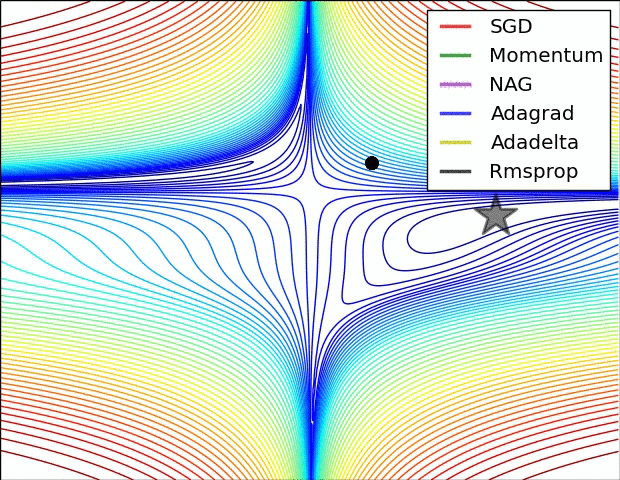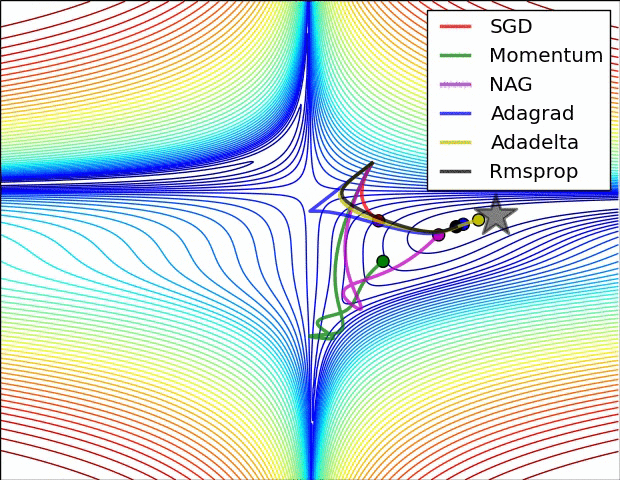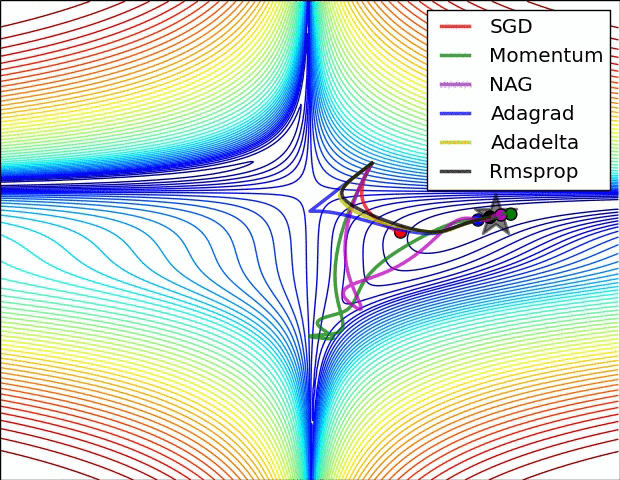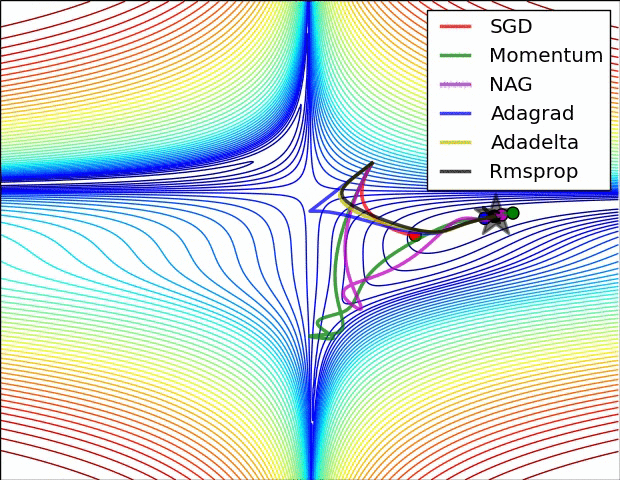
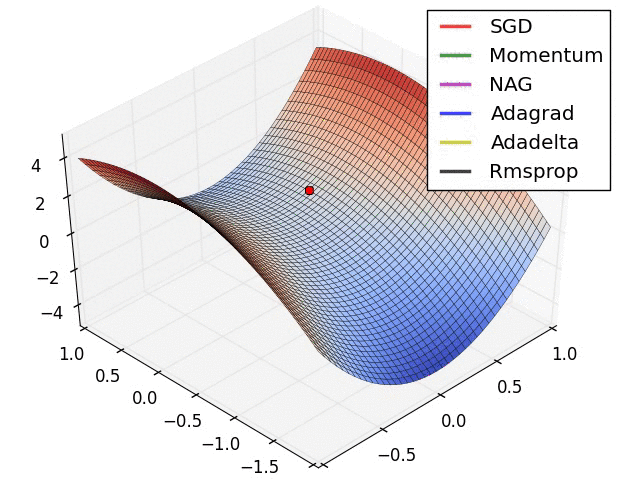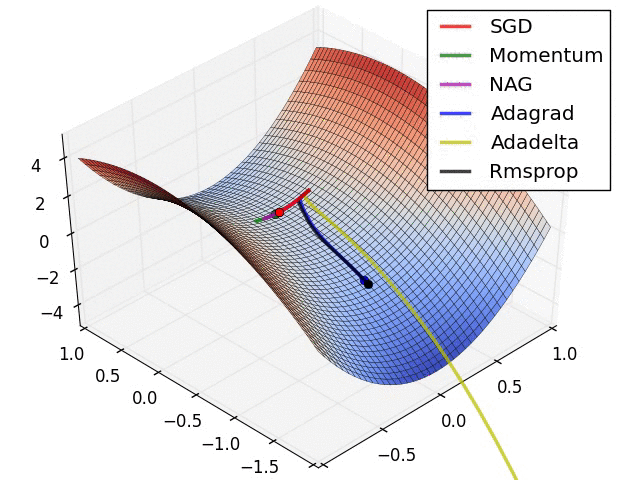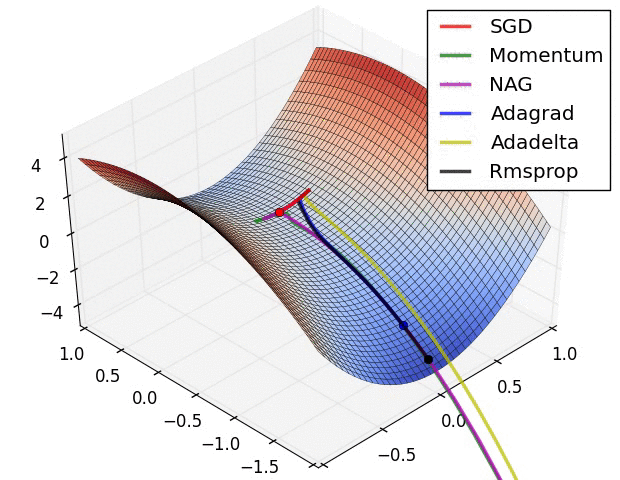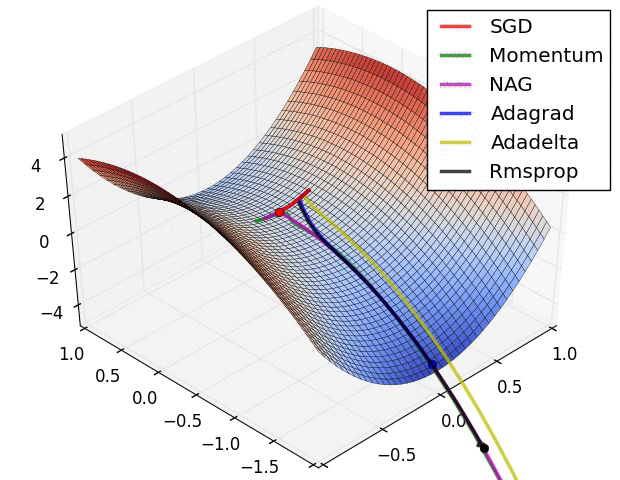
最適化#

SGD
Momentum
RMSProp
Adagrad
Adam
KFac

結合パターン#

完全結合
畳込み
Dilated
再帰結合
スキップコネクト，残渣

損失関数#

交差エントロピー
敵対学習
変分原理
最尤法
L2

ハイパーパラメータ#

学習率
層数
バッチサイズ
ドロップアウト率
初期化
データ拡張
勾配クリップ
モーメント

自分の Windows で環境構築するには#

パッケージマネージャは Chocolatey, Mac なら homebrew
Python 環境は anaconda, もしくはminiconda
Pythonのバージョンは 2.7 系と 3 系とありますが，3 系で良いでしょう
Python をブラウザ上で動作させるためには jupyter notebook anaconda もしくは chocolatory, homebrew からインストールできます。ananconda などを用いることで複雑なライブラリ間の依存関係を吸収することができます。
Jupyter notebook のクラウド環境は Google Colaboartory
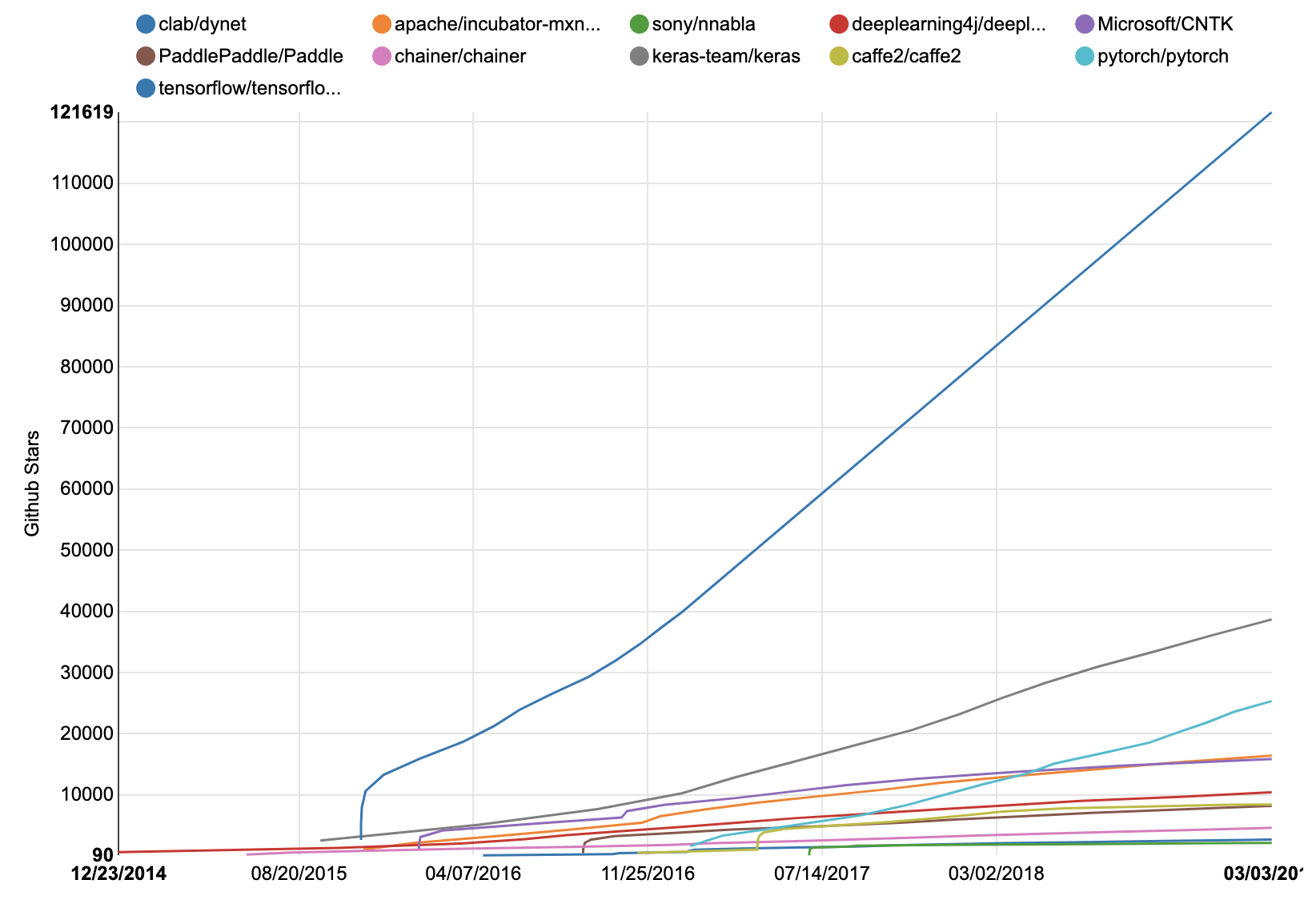
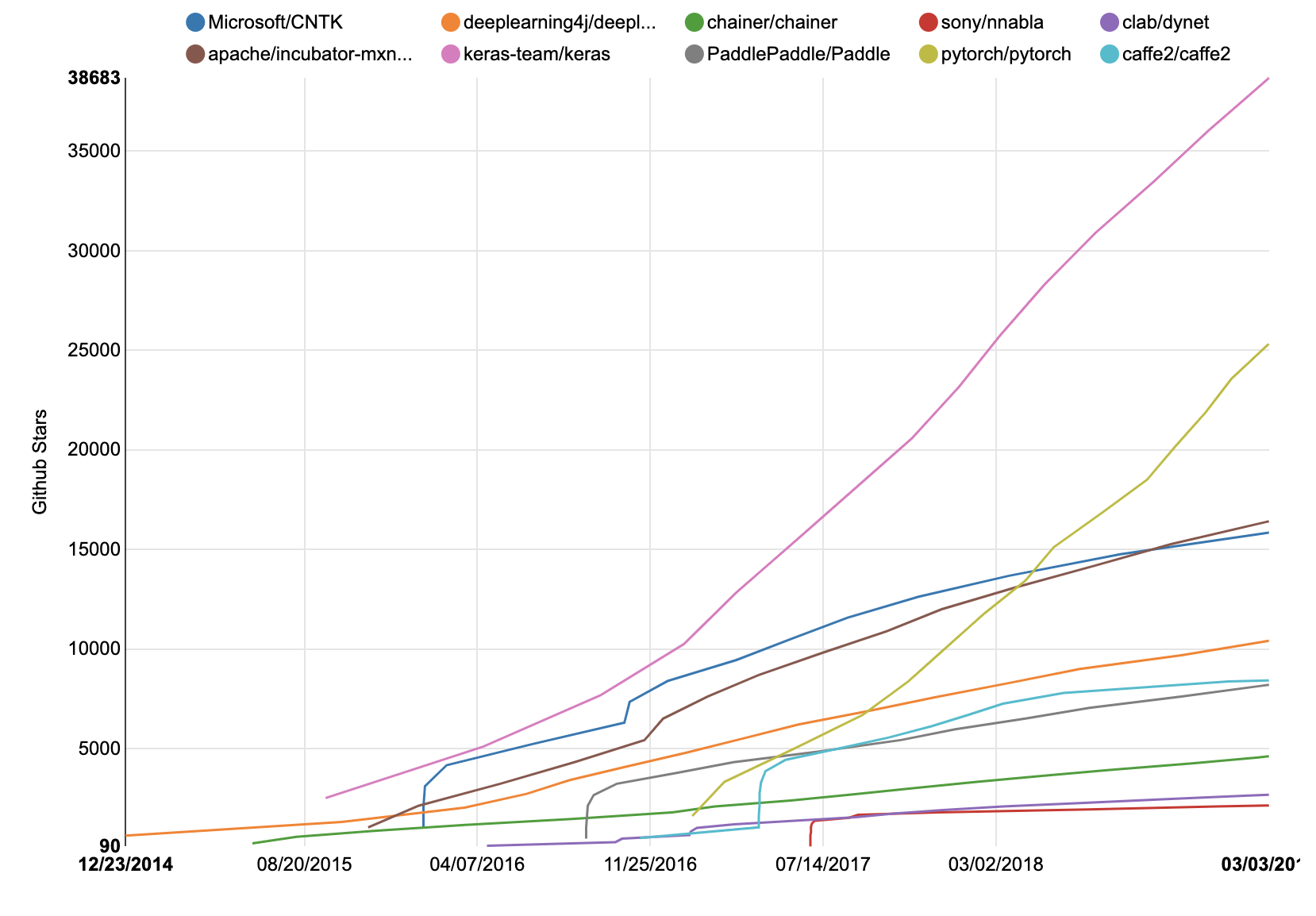
Python 上で動作するディープラーニング(深層学習)のフレームワークには，Tensorflow, keras, PyTorch などがあります。
その他にも数多くのフレームワークが存在しますが，GitHub での星の数のグラフを見てください。 TensorFlow が圧倒的であることがわかります。
TensorFlow を除いてプロットしてみるとそれ以外のフレームワークの動向を見てみると Keras と PyTorch が注目すべきであることがわかります。

資料#

学習済みのモデルを再利用するためには TensorFlow Hub
参考資料: Stackoverflow の言語トレンド
Python の初歩
PCA と tSNE との比較 kmninst を用いて