今、次の主張を考えます。
20歳以上の日本人男性の平均身長は166.0cmである。
つまり、母平均は166.0だという主張ですが、この主張は否定されるべきでしょうか。
前回の授業で、20歳以上の日本人男性の平均身長について、母平均の区間推定を行いました。 そのときの結果は、信頼度95%の信頼区間が[166.3, 166.9]でした。 主張の166.0はこの信頼区間の外側なので、この主張は95%の確率で否定されるべきというのが結論です。
ただ、主張を否定するためだけに信頼区間を計算するのは無駄です。 信頼区間の計算を思い出すと、信頼度95%の場合、標本の大きさ n , 標本平均 m , 標本標準偏差 s として、
[ m −1.96× s /√ n , m +1.96× s /√ n ]
でした。 つまり、信頼区間の下限と上限は、標本平均 m から標準誤差 s /√ n の1.96倍離れているということです。 したがって、この区間に主張の母平均μ 0 が入るかどうかは、母平均が標本平均から標準誤差の何倍離れているかを
z =( m −μ 0 )/( s /√ n )
で計算し、 z と1.96を比較すれば分かるのです。
実際、 n =3022, m =166.6, s =7.2, μ 0 =166.0 なので、
z =(166.6−166.0)/(7.2/√3022)=0.6/0.131=4.58
となり、4.58倍離れていることになります。 これは、1.96よりずっと大きいので、95%の確率で、母平均が166.0という主張は否定されるべきなのです。
仮説検定 とは、母集団に関する仮説を立て、標本を調査することによって、仮説を否定したりしなかったりすることです。
仮説とは、例えば
のようなものです。
仮説を否定することを、仮説を 棄却 すると言います。 仮説を肯定することを、仮説を 採択 すると言います。
缶ジュースの例で言えば、A社のすべての缶ジュースを調べるわけにはいかないので、標本調査を行うことになります。 標本を調べても、ピッタリ350mlになる訳はなく、多少の誤差はあるはずです。 しかし、誤差と呼べないほどの差が出たら、350mlであるという仮説は棄却して、缶ジュース製造機の故障を疑ったほうがよいでしょう。
仮説検定では、誤差の範囲内かどうかを判断するために、確率を用います。 確率を例えば5%と設定し、確率5%以下しか発生しない差が出たら、それは誤差ではなく、意味のある差だと結論付けます。 この5%を 有意水準 と言います。
仮説検定では、帰無仮説 H 0 と対立仮説 H 1 という2つの仮説を立てます。 帰無仮説 は、棄却すること目的とした仮説です。 対立仮説 は、帰無仮説の反対の内容になります。
缶ジュースの例では、
帰無仮説 H 0 : 母平均は350mlである(μ=350)
対立仮説 H 1 : 母平均は350mlでない(μ≠350)
となります。
帰無仮説が有意水準を下回る確率でしか起こりえない場合、帰無仮説は棄却され、対立仮説が採択されます。 逆に、帰無仮説が有意水準を上回る確率で起こりえる場合、帰無仮説は棄却されません。
ここからは、特に母平均の仮説検定について考えます。 つまり、
帰無仮説 H 0 : 母平均はμ 0 である(μ=μ 0 )
対立仮説 H 1 : 母平均はμ 0 でない(μ≠μ 0 )
という仮説です。 缶ジュースの例も、このパターンです。
母平均の仮説検定は、標本の大きさが大きいときと小さいときに分かれます。 標本が大きいときは、正規分布に基づいて検定します。 標本が小さいときは、 t 分布に基づいて検定します。 この節では、正規分布の場合について説明し、 t 分布の場合については次節で説明します。
正規分布の両側5%点が1.96であることを思い出してください。 有意水準が5%の場合、標本の大きさ n , 標本平均 m , 標本標準偏差 s として、母平均が標本平均から標準誤差の何倍離れているかを
z =( m −μ 0 )/( s /√ n )
で計算します。 そして、 z (の絶対値)が1.96より大きいならば、確率5%以下しか発生しない差が出たので、帰無仮説を棄却して対立仮説を採択します。 z (の絶対値)が1.96以下ならば、帰無仮説を棄却しません。
缶ジュースの例では、母平均が350mlかどうかが問題で、350mlより大きくても350mlより小さくても区別しませんでした。 これに対して、より大きい(あるいはより小さい)かどうかが問題になる場合があります。 上記の例では、
これは、母比率πが0.5より大きいかどうかを問題にしています。 この場合、仮説は
帰無仮説 H 0 : 母比率は0.5である(π=0.5)
対立仮説 H 1 : 母比率は0.5より大きい(π>0.5)
となります。 また、正規分布の両側5%点1.96の代わりに、片側5%点1.645を使います。 この値は、ExcelではNORMSINV(0.95)で求められます。
このように、ある値かどうかが問題で、より大きくてもより小さくても区別しない検定を 両側検定 と呼び、より大きい(あるいはより小さい)かどうかを問題にする検定を 片側検定 と呼びます。
母平均の仮説検定で、標本が小さい場合は、正規分布の代わりに t 分布を使います。 t 分布に基づいた仮説検定を、 t 検定 と呼びます。
有意水準が5%の場合、標本の大きさ n , 標本平均 m , 標本標準偏差 s として、母平均が標本平均から標準誤差の何倍離れているかを
t =( m −μ 0 )/( s /√ n )
で計算します。 この値を t 統計量 ( t 値)と呼びます。 次に、自由度 n −1 の t 分布の両側5%点 t 0.05 ( n −1) を、Excelの関数TINV(0.05, n - 1) で求めます。 最後に、 t (の絶対値)が t 0.05 ( n −1) より大きいならば、確率5%以下しか発生しない差が出たので、帰無仮説を棄却して対立仮説を採択します。 t (の絶対値)が t 0.05 ( n −1) 以下ならば、帰無仮説を棄却しません。
片側検定の場合は、両側5%点 t 0.05 ( n −1) の代わりに、片側5%点 t 0.1 ( n −1) を使います。 片側5%点は、Excelの関数TINV(0.1, n - 1) で求めます。
前回の授業では、母比率の区間推定を行いました。 母比率の仮説検定についても、同じように考えられます。 例えば、100人中60人が賛成する議題は、日本全国で過半数が賛成すると考えてよいか、などです。
簡単に言うと、仮説の母比率π, 標本比率 p に対して、母平均π, 標本平均 p , 母標準偏差を√(π×(1−π))とすると、標本が大きな場合の方法で仮説検定ができます。
なお、母比率の区間推定と母比率の仮説検定とでは、標準偏差の部分が異なっています。 これは、区間推定では母平均πが使えないので、母標準偏差√(π×(1−π))の代わりに標本標準偏差√( p ×(1− p ))にしたのです。
1種類のデータの仮説検定もそれなりに意味はありますが、応用上重要なのは、2種類のデータの仮説検定です。
例えば、ある製薬会社が、血圧を下げると考えられる飲料を開発したとします。 本当に血圧が下がるのかを調べるには、次の2種類の方法があります。
(1) 協力者全員にその飲料を飲んでもらい、飲む前と飲んだ後の血圧を測定する。
(2) 協力者を2つのグループに分け、一方にはその飲料を飲んでもらい、他方にはその飲料のニセモノを飲んでもらう。 その後、両方のグループの血圧を測定する。
どちらも2種類のデータが得られますが、前者は同一人物の前後のデータです。 これを 対標本 (ついひょうほん)と呼びます。 それに対して、後者は他人同士のデータです。 これを 2標本 と呼びます。
今日は、対標本の検定を行います。 2 標本の検定は次回行います。
実は、対標本は、本質的に1種類のデータです。 実際、前後のデータの差を計算し、差がゼロという帰無仮説のもとで検定を行えばよいのです。 しかし、応用上重要ということで、Excelの分析ツールを使って検定を行うことができます。
それでは、Excelを利用して、仮説検定を行いましょう。 以下のExcelファイルをダウンロードしてください。
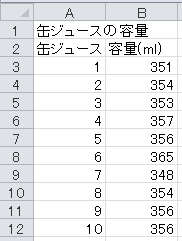
comp2j_09_data.xls最初のデータは、缶ジュースの容量についてです。 帰無仮説は母平均が350である、対立仮説は母平均が350でないとします。 有意水準5%で両側検定を行います。

まず、セルA13から下に、「仮説」、「標本の大きさ」、「平均」、「標準偏差」、「標準誤差」、「t」、「自由度」、「両側5%点」と入力します。 仮説の350も入力します。
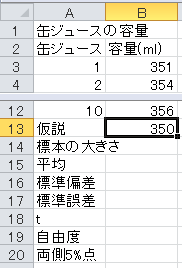
標本の大きさはExcelのCOUNT関数で求められます。 セルB14に=COUNT(B3:B12)と入力します。
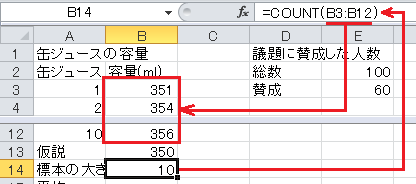
平均はExcelのAVERAGE関数で求められます。 セルB15に=AVERAGE(B3:B12)と入力します。
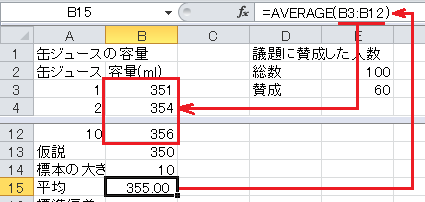
標準偏差はExcelのSTDEV関数で求められます。 セルB16に=STDEV(B3:B12)と入力します。
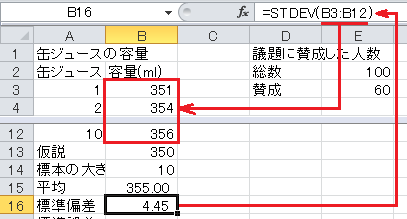
標準誤差=標準偏差/√標本の大きさ、なので、セルB17に=B16/SQRT(B14)と入力します。
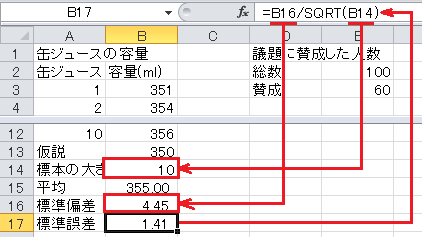
t =(平均−仮説)/標準誤差、なので、セルB18に=(B15-B13)/B17と入力します。
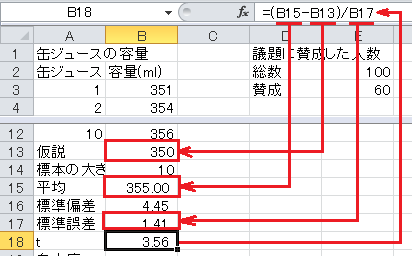
自由度=標本の大きさ−1, なので、セルB19に=B14-1と入力します。
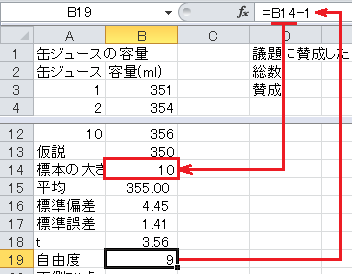
t 分布の両側5%点はExcelのTINV関数で求められます。 関数の形式はTINV(確率, 自由度)なので、セルB20に=TINV(0.05,B19)と入力します。
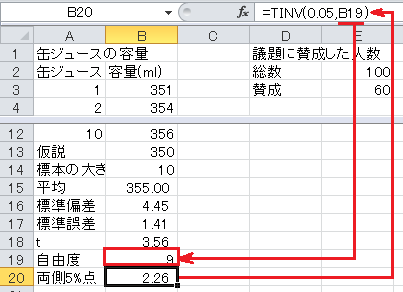
最後に t の値と両側5%点を比較します。
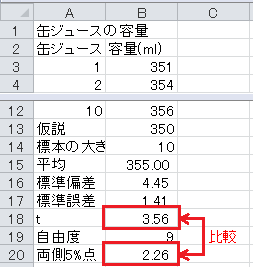
t の値が両側5%点より大きいので、帰無仮説が棄却され、対立仮説が採択されます。 従って、350mlではないということになります。
議題に賛成した人数の場合は、帰無仮説は母比率が50%, 対立仮説は母比率が過半数(50%を超える)とします。 有意水準5%で片側検定を行います。
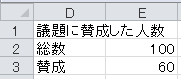
まず、セルD4から下に、「仮説」、「比率」、「標準偏差」、「標準誤差」、「z」、「片側5%点」と入力します。 仮説の0.5および正規分布の片側5%点の1.645も入力しておきます。
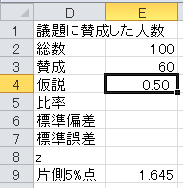
比率=賛成/総数、なので、セルE5に=E3/E2と入力します。
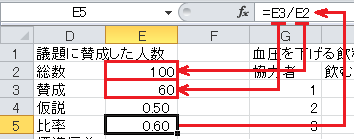
標準偏差=√(仮説×(1−仮説)), なので、セルE6に=SQRT(E4*(1-E4))と入力します。
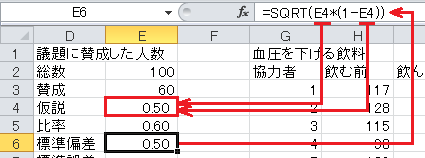
標準誤差=標準偏差/√総数、なので、セルE7に=E6/SQRT(E2)と入力します。
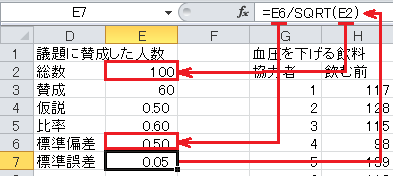
z =(比率−仮説)/標準誤差、なので、セルE8に=(E5-E4)/E7と入力します。
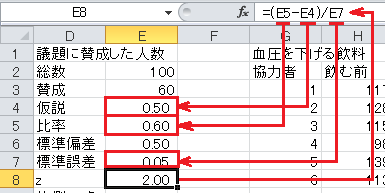
最後に z の値と片側5%点を比較します。
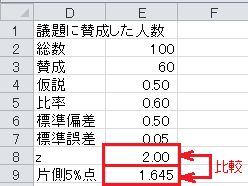
z の値が片側5%点より大きいので、帰無仮説は棄却できます。 従って、過半数が賛成していると言えます。
血圧を下げる飲料の場合、帰無仮説は血圧が変わらない、対立仮説は血圧が下がるです。 有意水準5%で片側検定を行います。
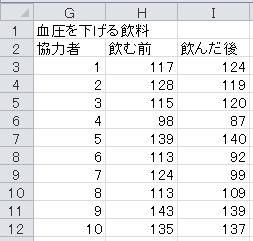
まず、メニューバーで「ツール」→「分析ツール」とクリックして、分析ツールのウィンドウを開きます。 「t 検定: 一対の標本による平均の検定」をクリックして、「OK」ボタンをクリックします。
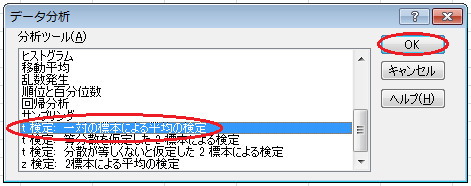
「変数 1 の入力範囲」に飲む前のデータ$H$2:$H$12を入力し、「変数 2 の入力範囲」に飲んだ後のデータ$I$2:$I$12を入力します。 「仮説平均との差異」は空欄のままにし、「ラベル」にチェックを入れ、「α」が0.05であることを確認します。 「出力オプション」の「出力先」をクリックし、空いているセル(例えば$G$14)を入力します。
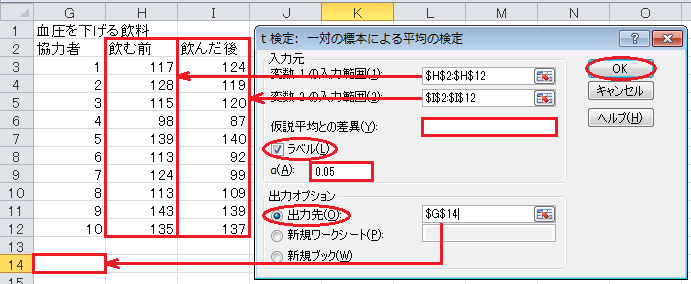
分析ツールの出力の読み方ですが、「t 境界値 片側」が片側5%点を表し、「t 境界値 両側」が両側5%点を表します。
最後に t の値と片側5%点を比較します。
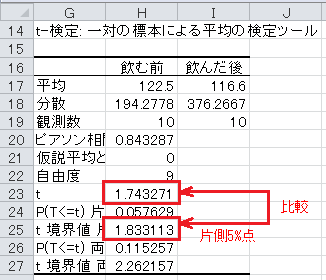
t の値が片側5%点より小さいので、帰無仮説は棄却できません。 したがって、この飲料は血圧を下げるとは言えないのです。
以下のファイルをダウンロードしてください。
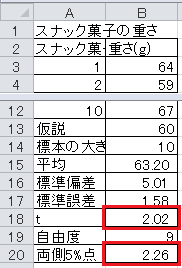
comp2j_09_report.xls(1)表「スナック菓子の重さ」は、ある食品メーカーのスナック菓子の重さが本当に60gかどうかを標本調査したものです。 帰無仮説は母平均が60であるとし、対立仮説は母平均が60でないとします。 有意水準5%で両側検定を行い、帰無仮説が棄却できるかどうかを答えてください。
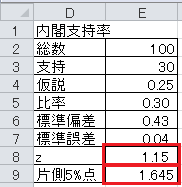
(2)表「内閣支持率」は、ランダムに選んだ100名に内閣を支持するかどうかを聞いたものです。 この調査から、内閣支持率は25%を超えていると言えるかどうかを考えます。 帰無仮説は母比率が0.25であるとし、対立仮説は母比率が0.25を超えるとします。 有意水準5%で片側検定を行い、帰無仮説が棄却できるかどうかを答えてください。
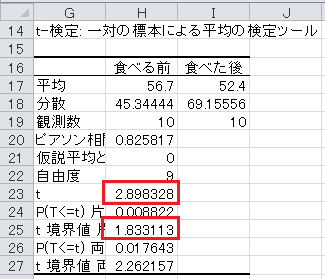
(3)表「ダイエット食品」は、あるダイエット食品を1か月間食べ続けてもらい、食べる前と食べた後の体重を測定したものです。 この調査から、このダイエット食品は効果があるかどうかを考えます。 帰無仮説は体重が変わらないとし、対立仮説は体重が減ったとします。 有意水準5%で片側検定を行い、帰無仮説が棄却できるかどうかを答えてください。
今日の演習9の答案(Excelファイル)をメールで提出してください。 差出人は学内のメール・アドレス(b08a001@cis.twcu.ac.jpなど)とし、宛先はkonishi@cis.twcu.ac.jpとします。 メールの本文には、学生番号、氏名、科目名、授業日(11月30日)を明記してください。