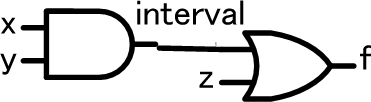
回路の真理値表を作成すること

xとyはまず最初にANDゲートに入力され、その結果がORゲートに入力されるので、ANDゲートの出力をintervalとすると、ORゲートへの入力は以下のようになります。
| x | y | z | interval |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
この表で、intervalとzをORゲートに入力した結果が解答となります。
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
回路の真理値表を作成すること
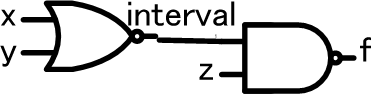
xとyはまず最初にNORゲートに入力され、その結果がNANDゲートに入力されるので、NORゲートの出力をintervalとすると、NANDゲートへの入力は以下のようになります。
| x | y | z | interval |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
この表で、intervalとzをNANDゲートに入力した結果が解答となります。
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
回路の真理値表を作成すること
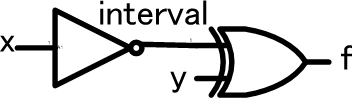
xはまず最初にNOTゲートに入力され、その結果がXORゲートに入力されるので、NOTゲートの出力をintervalとすると、XORゲートへの入力は以下のようになります。
| x | y | interval |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
この表で、intervalとyをXORゲートに入力した結果が解答となります。
| x | y | f |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 入力 | 出力 | ||||
|---|---|---|---|---|---|
| xi(i桁目の足す数) | yi(i桁目の足される数) | ci-1(i桁目の1つ前の桁の足し算の結果の繰り上がり) | ci(i桁目の足し算の結果の繰り上がり) | fi(i桁目の足し算の結果) | |
| (1) | 0 | 0 | 0 | 0 | 0 |
| (2) | 0 | 1 | 0 | 0 | 1 |
| (3) | 1 | 0 | 0 | 0 | 1 |
| (4) | 1 | 1 | 0 | 1 | 0 |
| (5) | 0 | 0 | 1 | 0 | 1 |
| (6) | 0 | 1 | 1 | 1 | 0 |
| (7) | 1 | 0 | 1 | 1 | 0 |
| (8) | 1 | 1 | 1 | 1 | 1 |
全加算器で2進数01101+01100の足し算をしてみて、結果が正しいことを確認しよう
01101+01100の計算は、5桁の足し算なので、加算回路は下図のようになります。
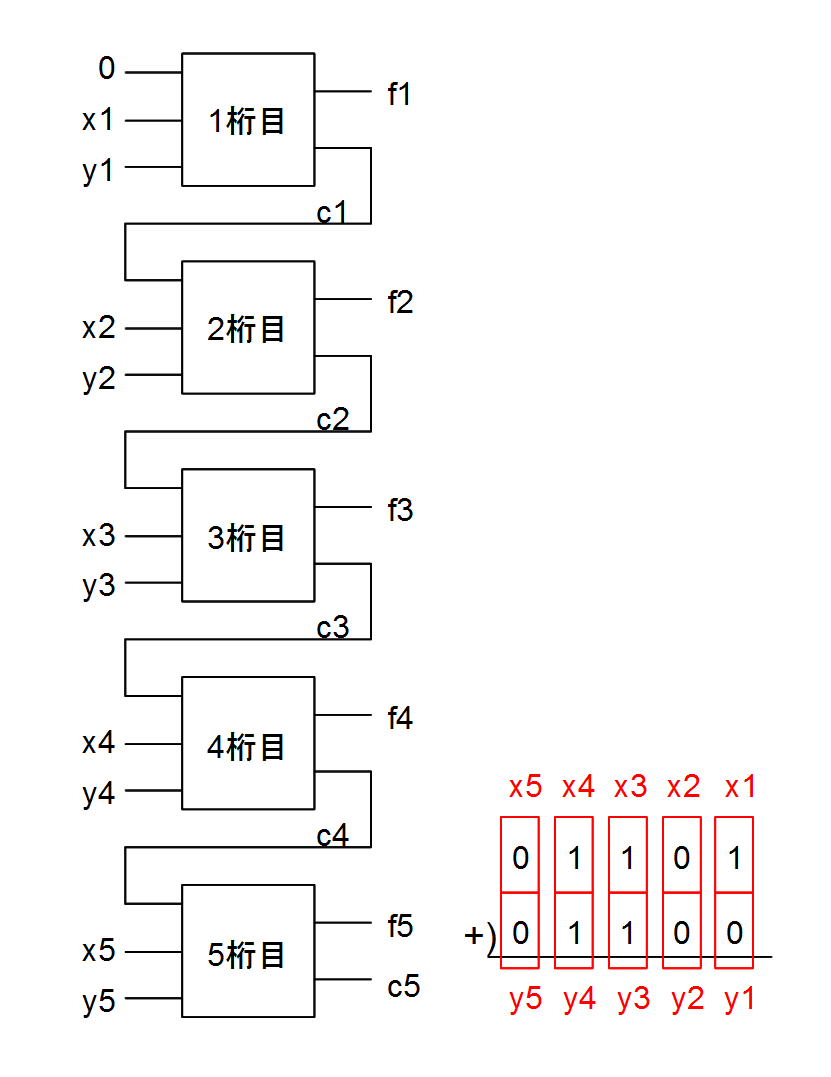
この足し算では、それぞれの桁の足し算の結果であるc(次の桁への繰り上がり)と、f(その桁の和)は、全加算器の真理値表から、下記のようになります。
この加算回路での処理の結果、f5~f1を並べたものが、足し算の結果になります。
加算回路の処理の結果: 11001
人間が01101+01100の足し算をすると、結果は11001になるので、加算回路での結果と、本来の足し算の結果は同じということが確認できました。
全加算器で2進数0011+0110の足し算をしてみて、結果が正しいことを確認しよう
0011+0110の計算は、4桁の足し算なので、加算回路は下図のようになります。
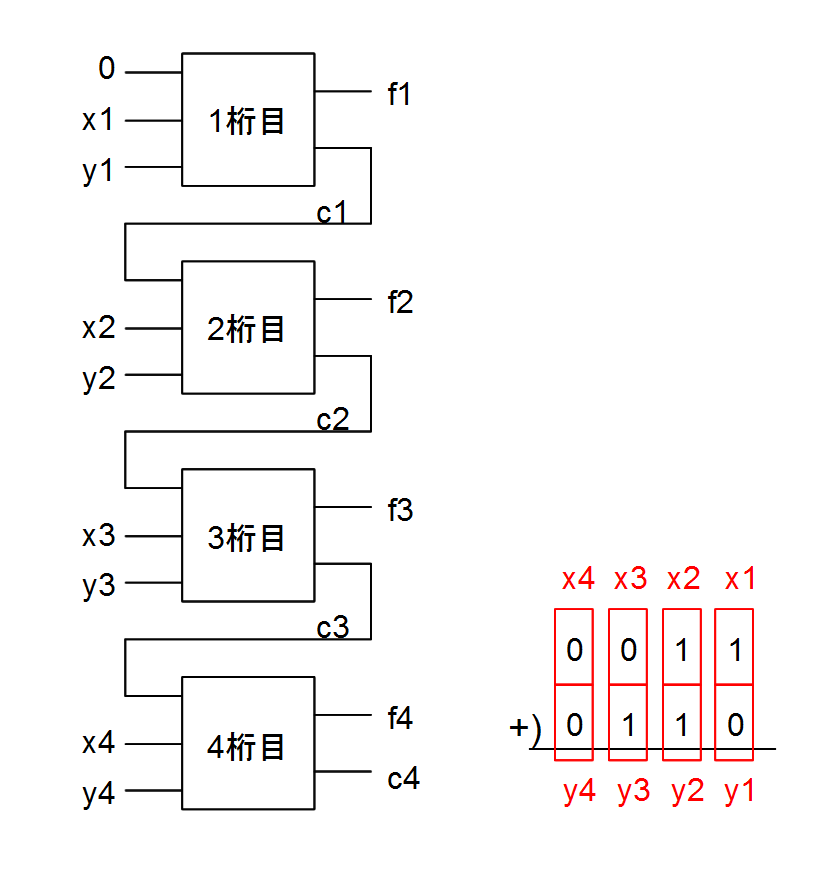
この足し算では、それぞれの桁の足し算の結果であるc(次の桁への繰り上がり)と、f(その桁の和)は、全加算器の真理値表から、下記のようになります。
この加算回路での処理の結果、f4~f1を並べたものが、足し算の結果になります。
加算回路の処理の結果: 1001
人間が0011+0110の足し算をすると、結果は1001になるので、加算回路での結果と、本来の足し算の結果は同じということが確認できました。
全加算器において、入力xが1、入力yが0、入力zが1のとき、出力c(繰り上げ)とf(和)はどれになるか(2009年度基本情報技術者試験 秋期問題より)
入力xが1、入力yが0、入力zが1なので、全加算器の真理値表の(7)の入力のパターンになります。従って、出力は、cが1、fが0となります。
解答: ウ
Copyright (C) Junko Shirogane, Tokyo Woman's Christian University 2015, All rights reserved.