ホップフィールドモデル

ホップフィールド(Hopfield) モデルの特徴は、

1. ユニット間の結合係数が対称。 ただし すなわち自己結合係数は存在しない
2. ユニットの状態変化は非同期的、一回に任意の一つのユニットしか状態 変化しない。

n 個の 2 値ユニットを考える 。 このネットワークの状態は 個存在し、 幾何学的には n 次元超立方体の頂点に対応する。 時刻 における ユニット i への入力を , 出力を とすれば 時刻 t+1 での出力 は、結合荷重 としきい値 を用いて次のように表現される

 

 

すなわち、各ユニットの i は、他のユニット j からの入力 の 重み付き和 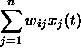がしきい値 より大きければ 1 を出力し、小さければ 0 を出力する。 ホップフィールドモデルでは、一回に一個のユニットしか変化しないことに注意。