勾配降下法の基礎#

勾配降下法とは，盲目のハイカー アナロジーが用いられます。 視覚障害者が白杖を頼りに山を下るイメージです。

from https://cdn-images-1.medium.com/max/1600/1*f9a162GhpMbiTVTAua_lLQ.png

勾配降下法の意味#

• 勾配降下法を用いるためには，誤差関数，コスト関数，損失関数，と呼ばれる 量を定義する必要があります。

• さまざまなコスト関数が提案されています。

• コスト関数を各変数で微分することで，局所最小値を探すことを学習と呼びます

勾配#

平均自乗誤差の場合であれば次式で与えられます。

$$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}\left(f_{\theta}\left(x^{(i)}-y^{(i)}\right)\right)^2.$$

上式を $\theta$ で微分すれば，

$$\frac{\partial}{\partial\theta_{j}}J\left(\theta\right)=\frac{2}{m}\sum_{i=1}^{m}\left(\theta^{\top}\mathbf{x}^{(i)}-y^{(i)}\right)x_j^{(i)},$$

を得ます。

学習率#

この微分情報に基づいて山を下っていきます。

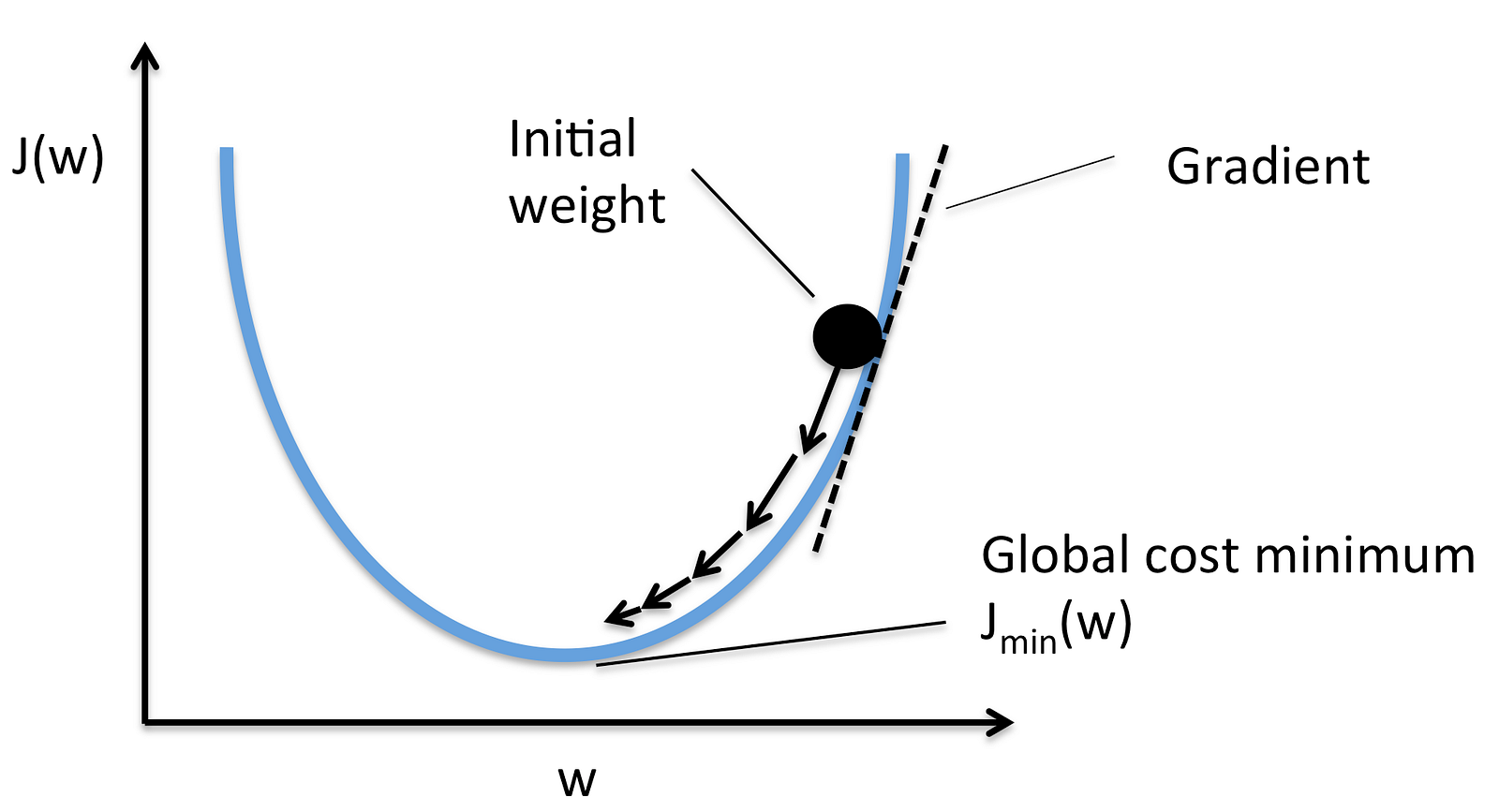
from https://cdn-images-1.medium.com/max/1600/0*rBQI7uBhBKE8KT-X.png

数式で表現すると漸化式として次式のように表現できます:

$$\theta_{j+1} = \theta_{j}-\alpha\frac{\partial}{\partial\theta_{j}}J\left(\theta\right),$$

$\alpha$ のとり方によっては学習が遅くなったり，発散したりします。 $\alpha$ を調整する手法がいくつか提案されています。

saddle points

勾配降下法の種類#

1. ミニバッチ: 全データをもちいずに，いくつかだけサンプリングして用いる商法です

2. 確率的勾配降下法: そのつど一つづつ更新する手法です <!--

3. [With every GD iteration, you need to shuffle the training set and pick a random training example from that.]
4. [Since, you're only using one training example, your path to the local minima will be very noisey like a drunk man after having one too many drinks.] -->
5. バッチ: 全データを用いる手法です

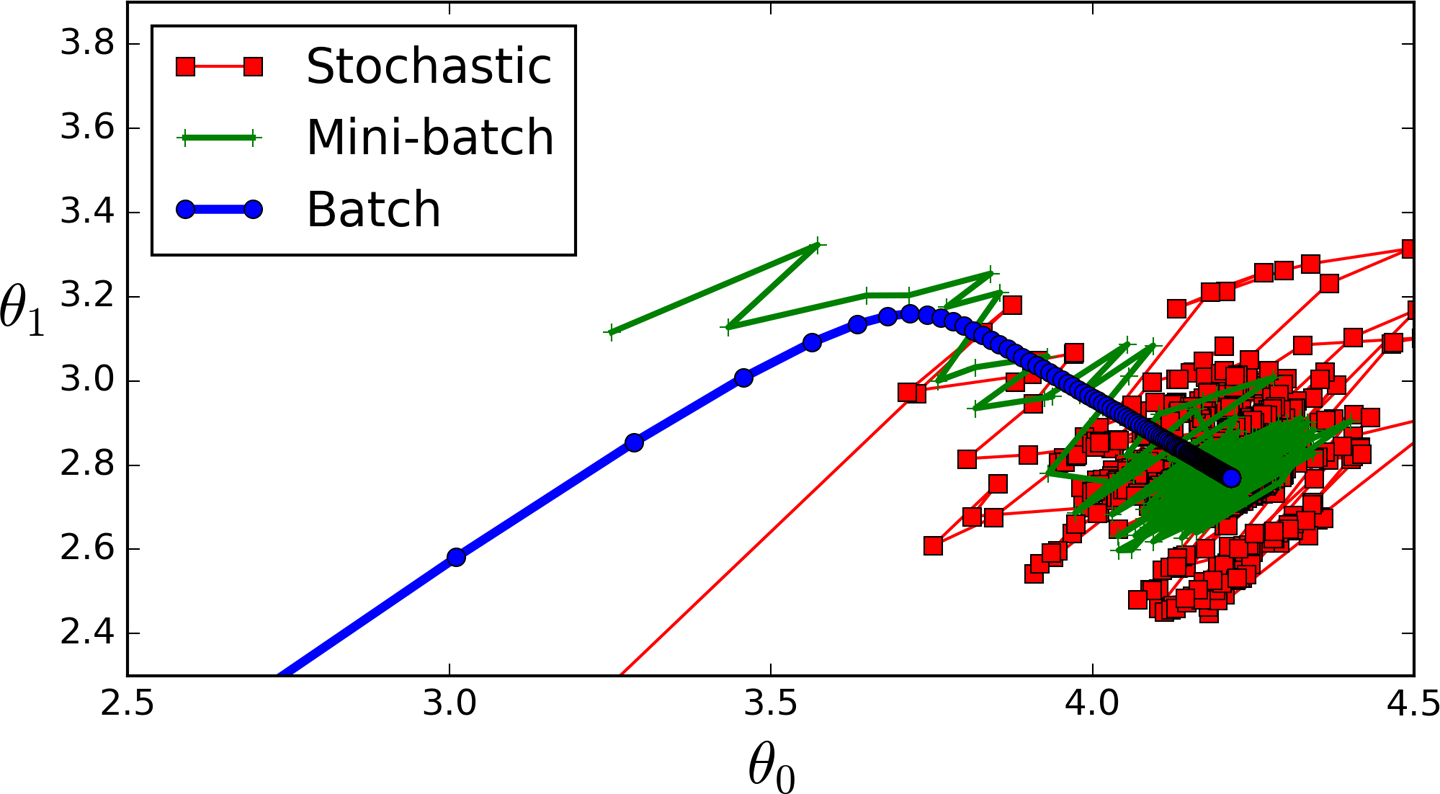from https://cdn-images-1.medium.com/max/1600/0*sFYJwQCCjOnXpSoD.png

実装#

def train(X, y, W, b, lr, max_iters):
    '''
    Performs GD on all training examples,

    X: Training data set,
    y: Labels for training data,
    W: Weights vector,
    b: Bias variable,
    lr: The learning rate,
    max_iters: Maximum GD iterations.
    '''

    dW = 0 # Weights gradient accumulator
    db = 0 # Bias gradient accumulator
    m = X.shape[0] # No. of training examples

    for i in range(max_iters):
        dW = 0 # Reseting the accumulators
        db = 0
        for j in range(m):
            # 1. Iterate over all examples,
            # 2. Compute gradients of the weights and biases in w_grad and b_grad,
            # 3. Update dW by adding w_grad and dB by adding b_grad,
         W -= lr * (dW / m) # Update the weights
         b -= lr * (db / m) # Update the bias

    return W, b # Return the updated weights and bias.